a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là các góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
\(\widehat{ABK}=\widehat{HBK}\)
Do đó: ΔBAK=ΔBHK
c: Ta có: ΔBAK=ΔBHK
=>KA=KH
Xét ΔKAI vuông tại A và ΔKHC vuông tại H có
KA=KH
AI=HC
Do đó: ΔKAI=ΔKHC
=>\(\widehat{AKI}=\widehat{HKC}\)
mà \(\widehat{HKC}+\widehat{AKH}=180^0\)(hai góc kề bù)
nên \(\widehat{AKH}+\widehat{AKI}=180^0\)
=>H,K,I thẳng hàng
d: Xét ΔBIC có \(\dfrac{BA}{AI}=\dfrac{BH}{HC}\)
nên AH//IC

 NHỚ LÀM THEO KIẾN THỨC LỚP 7 NHA!! CẢM ƠN Ạ!
NHỚ LÀM THEO KIẾN THỨC LỚP 7 NHA!! CẢM ƠN Ạ!



 Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều





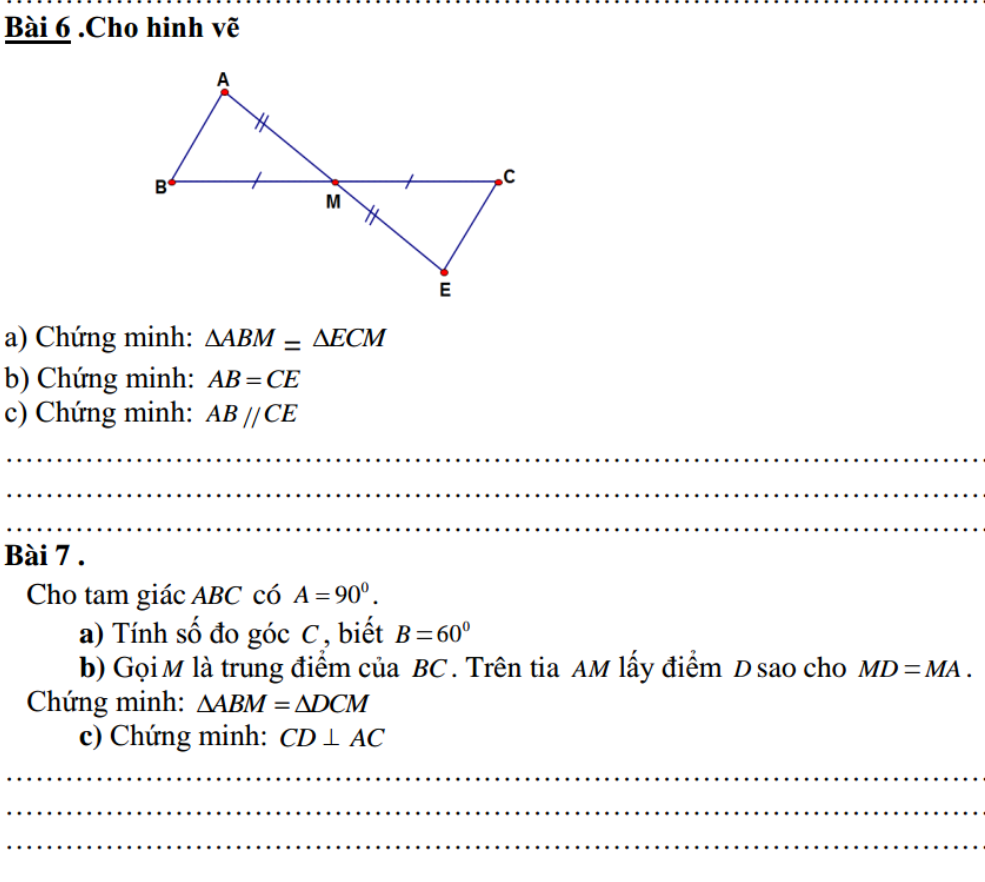





 các bạn giải hộ mik nha,cảm ơn ơn các bạn nhiều !!!
các bạn giải hộ mik nha,cảm ơn ơn các bạn nhiều !!!
