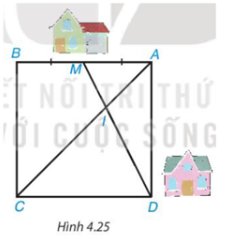
Theo đề bài, ABCD là hình vuông nên AB = AD và AC là tia phân giác của \(\widehat {BA{\rm{D}}}\)
Vì M là trung điểm của AB nên \(AM = BM = \dfrac{1}{2}AB = \dfrac{1}{2}A{\rm{D}}\) hay \(\dfrac{{AM}}{{A{\rm{D}}}} = \dfrac{1}{2}\)
Vì AC là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay AI là tia phân giác của \(\widehat {MA{\rm{D}}}\), áp dụng tính chất đường phân giác trong tam giác ADM, ta có:
\(\dfrac{{AM}}{{A{\rm{D}}}} = \dfrac{{IM}}{{I{\rm{D}}}} = \dfrac{1}{2}\) suy ra ID = 2IM.
Giả sử vận tốc đi bộ của bạn Mai và bạn Dung đều bằng nhau.
Theo đề bài, I là địa điểm gặp nhau nên bạn Mai đi theo quãng đường MI, bạn Dung đi theo quãng đường DI.
Vì quãng đường bạn Dung đi gấp 2 lần quãng đường bạn Mai đi và vận tốc đi bộ của hai bạn đều bằng nhau (giả sử) nên thời gian bạn Dung đi gấp 2 lần thời gian bạn Mai đi thì hai bạn mới gặp nhau tại địa điểm I.
Bạn Dung gặp bạn Mai lúc 7h30 nên thời gian bạn Mai đi trên quãng đường MI là:
7h30 – 7h = 30 phút.
Khi đó, thời gian bạn Dung đi là 1h. Do đó, bạn Dung xuất phát từ lúc:
7h30 – 1h = 6h30.
Vậy bạn Dung xuất phát lúc 6h30 để gặp bạn Mai lúc 7h30 tại điểm I.