Question

Cho tam giác ABC. Đường phân giác trong của góc A cắt BC tại D. Tính độ dài đoạn thẳng DC biết AB = 4,5 m; AC = 7,0 m và CB = 3,5 m (làm tròn kết quả đến hàng phần chục).

Answer 1

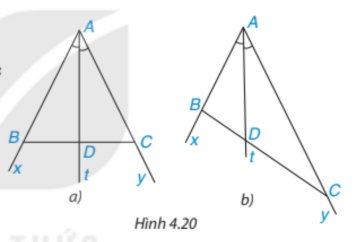
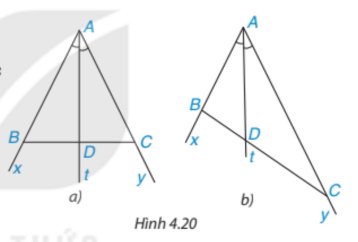
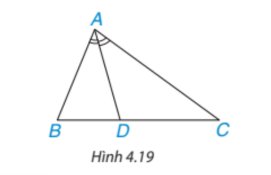
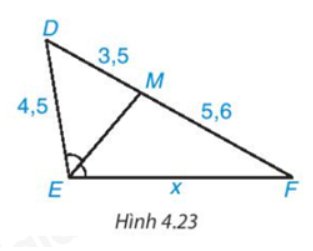
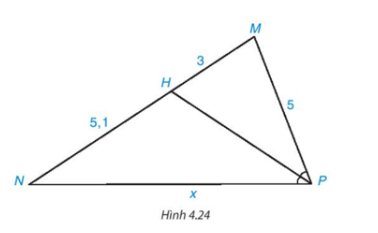
Theo đề bài, đường phân giác trong của góc A cắt BC tại D nên AD là tia phân giác của \(\widehat {BAC}\).

Áp dụng tính chất đường phân giác của tam giác, ta có:

\(\dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DC}}\) hay \(\dfrac{{4,5}}{7} = \dfrac{{DB}}{{DC}}\).

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{{DB}}{{4,5}} = \dfrac{{DC}}{7} = \dfrac{{DB + DC}}{{4.5 + 7}} = \dfrac{{BC}}{{11,5}} = \dfrac{{3,5}}{{11,5}} = \dfrac{7}{{23}}\)

Suy ra \(DC = \dfrac{{7.7}}{{23}} = \dfrac{{49}}{{23}} \) ≈ 2,1 (m)

Vậy DC ≈ 2,1 m.