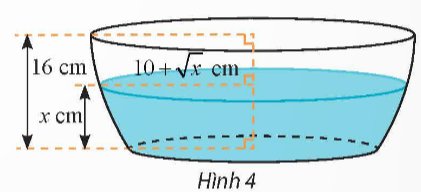
Chọn trục \(Ox\) sao cho \(O\) trùng với tâm của đáy, chiều dương của trục là chiều hướng lên trên.
Khi cắt chậu nước bằng mặt phẳng song song với đáy và cách mặt đáy \(x\), thì mặt phẳng đó cắt trục \(Ox\) tại điểm có hoành độ \(x\). Mặt cắt là hình tròn có bán kính \(\left( {10 + \sqrt x } \right)\) (cm)
Như vậy, diện tích mặt cắt là \(S\left( x \right) = \pi {\left( {10 + \sqrt x } \right)^2} = \pi \left( {x + 100 + 20\sqrt x } \right)\).
Suy ra dung tích của chậu là
\(V = \int\limits_0^{16} {S\left( x \right)dx} = \int\limits_0^{16} {\pi \left( {x + 100 + 20\sqrt x } \right)dx} = \pi \left. {\left( {\frac{{{x^2}}}{2} + 100x + 20.\frac{2}{3}\sqrt {{x^3}} } \right)} \right|_0^{16} = \frac{{7744}}{3}\pi \) (\({\rm{c}}{{\rm{m}}^3}\)).