Một ô tô có khối lượng 2 tấn khi đi qua A có vận tốc là 72 km/h thì tài xế tắt máy, xe chuyển động chậm dần đến B thì có vận tốc 18 km/h. Biết quãng đường AB nằm ngang dài 100 m
a, Xác định hệ số ma sát trên đoạn đường AB.
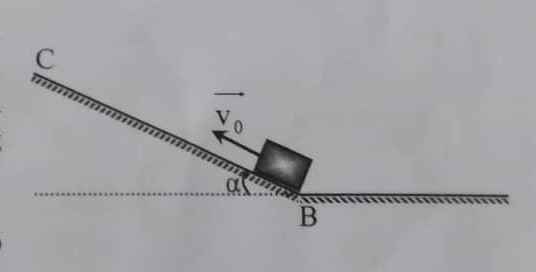
b, Đến B vẫn không nổ máy và tiếp tục xuống một dốc nghiêng BC dài 50 m hợp với mặt phẳng nằm ngang một góc 30o. Biết hệ số ma sát giữa bánh xe và dốc nghiêng là 0,1. Xác định vận tốc của xe tại trên dốc nghiêng C.
c, Đến C xe nổ máy và chuyển động thẳng đều lên dốc CD dài 20 m có góc nghiêng 45o so với mặt phẳng nằm ngang. Tính công mà lực kéo động cơ thực hiện trên dốc này.
Lấy g = 10 m/s2.☺☺
a/ Gia tốc của xe là:
\(v^2-v_0^2=2aS\Leftrightarrow5^2-20^2=2a.100\)
\(\Leftrightarrow a=-1,875\left(m/s^2\right)\)
Có \(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
\(\Rightarrow-\mu mg=m.a\Leftrightarrow\mu=\frac{-1,875}{-10}=0,1875\)
b/ Có \(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
\(\Rightarrow\left\{{}\begin{matrix}Ox:P.\sin\alpha-F_{ms}=m.a\\Oy:N=P.\cos\alpha\end{matrix}\right.\)
\(\Rightarrow mg\sin\alpha-\mu mg.\cos\alpha=m.a\)
\(\Leftrightarrow a=10.\frac{1}{2}-0,1.10.\frac{\sqrt{3}}{2}\approx4,1\left(m/s^2\right)\)
\(v^2-v_0^2=2aS\Leftrightarrow v=\sqrt{5^2+2.4,1.50}\approx20,8\left(m/s\right)\)
c/ \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{0}\)
\(\Rightarrow F=P.\sin\alpha=mg\sin\alpha=20000.\frac{\sqrt{2}}{2}=10000\sqrt{2}\left(N\right)\)
\(\Rightarrow A_F=F.s=10000\sqrt{2}.20=200000\sqrt{2}\left(J\right)\)