Ta có \({Q_1} = 56;{Q_3} = 84\)
\({\Delta _Q} = {Q_3} - {Q_1} = 84 - 56 = 28\)
\({Q_1} - 1,5{\Delta _Q} = 56 - 1,5.28 = 14\)
\({Q_3} + 1,5.{\Delta _Q} = 84 - 1,5.28 = 126\)
Ta thấy 10 < 14 nên 10 là giá trị bất thường
Ta có \({Q_1} = 56;{Q_3} = 84\)
\({\Delta _Q} = {Q_3} - {Q_1} = 84 - 56 = 28\)
\({Q_1} - 1,5{\Delta _Q} = 56 - 1,5.28 = 14\)
\({Q_3} + 1,5.{\Delta _Q} = 84 - 1,5.28 = 126\)
Ta thấy 10 < 14 nên 10 là giá trị bất thường
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán (khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn) sẽ thay đổi như thế nào nếu:
a) Nhân mỗi giá trị của mẫu số liệu với 2.
b) Cộng mỗi giá trị của mẫu số liệu với 2.
Tỉ lệ thất nghiệp ở một số quốc gia vào năm 2007 (đơn vị %) được cho như sau:
7,8 3,2 7,7 8,7 8,6 8,4 7,2 3,6
5,0 4,4 6,7 7,0 4,5 6,0 5,4
Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.
Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được:
Giá trị nhỏ nhất bằng 2,5;\({Q_1} = 36\), \({Q_2} = 60\),\({Q_3} = 100\); giá trị lớn nhất bằng 205.
a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu?
b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này.
c) Tìm khoảng tứ phân vị của mẫu số liệu.
Mỗi khẳng định sau đúng hay sai?
(1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn.
(2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại.
(3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất.
(4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp.
(5) Các số đo độ phân tán đều không âm.
Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của An:
12 7 10 9 12 9 10 11 10 14.
Hãy tìm khoảng tứ phân vị cho mẫu số liệu này.
Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387
Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.
Trong một tuần, nhiệt độ cao nhất trong ngày (đơn vị C) tại hai thành phố Hà Nội và Điện Biên được cho như sau:
Hà Nội: 23 25 28 28 32 33 35.
Điện Biên: 16 24 26 26 26 27 28.
a) Tính các khoảng biến thiên của mỗi mẫu số liệu và so sánh.
b) Em có nhận xét gì về sự ảnh hưởng của giá trị 16 đến khoảng biến thiên của mẫu số liệu về nhiệt độ cao nhất trong ngày tại Điện Biên?
c) Tính các tứ phân vị và hiệu \({Q_3} - {Q_1}\) cho mỗi mẫu số liệu. Có thể dùng hiệu này để đo độ phân tán của mẫu số liệu không?
Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:
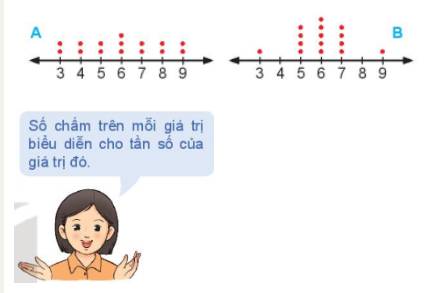
Không tính toán, hãy cho biết:
a) Hai mẫu số liệu này có cùng khoảng biến thiên và số trung bình không?
b) Mẫu số liệu nào có phương sai lớn hơn?
Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161
Tính khoảng biến thiên của mẫu số liệu này.