Question

Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác đều ở Hình 3a được vẽ lại như Hình 3b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng (A'B'C').

Answer 1

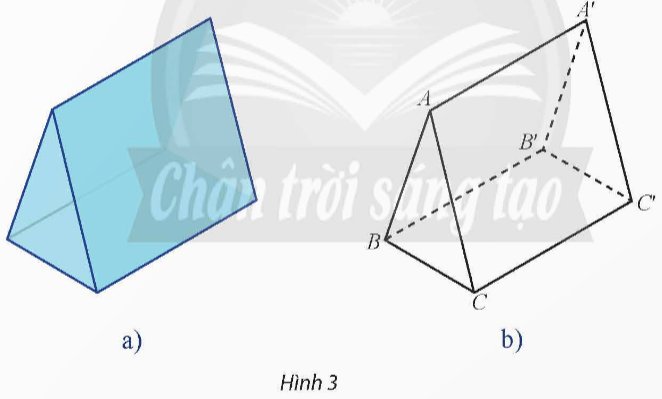
Ta thấy rằng \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {A'B'C'} \right)\). Suy ra \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\).

Do \(ABC.A'B'C'\) là lăng trụ đứng, nên ta có \(BB' \bot \left( {A'B'C'} \right)\).

Mặt khác, vectơ \(\overrightarrow {BB'} \) có giá là đường thẳng \(BB'\), do đó \(\overrightarrow {BB'} \) là một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).