Khi hai tam giác có thể trồng khít lên nhau thì các cạnh tương ứng của hai tam giác bằng nhau và các góc tương ứng của hai tam giác bằng nhau.
Bài 3. Hai tam giác bằng nhau
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).a) So sánh:- Các cặp cạnh: AB và A’B’; BC và B’C’; CA và C’A’.- Các cặp góc: A và A’; B và B’; C và C’.b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không?c) Cắt mảnh giấy hình tam giác ABC và mảnh giất hình tam giác A’B’C’, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?
Đọc tiếp
Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).
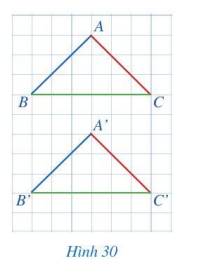
a) So sánh:
- Các cặp cạnh: AB và A’B’; BC và B’C’; CA và C’A’.
- Các cặp góc: A và A’; B và B’; C và C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không?
c) Cắt mảnh giấy hình tam giác ABC và mảnh giất hình tam giác A’B’C’, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?
Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn \(\Delta AMB = \Delta AMC\)(Hình 32). Chứng minh rằng:
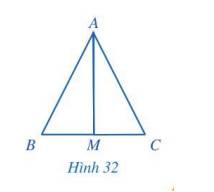
a) M là trung điểm của đoạn thẳng BC.
b) Tia AM là tia phân giác của góc BAC và \(AM \bot BC\).
Cho biết \(\Delta ABC = \Delta DEG\),\(AB = 3\)cm,\(BC = 4\)cm,\(CA = 6\)cm. Tìm độ dài các cạnh của tam giác DEG.
Cho biết \(\Delta PQR = \Delta IHK\),\(\widehat P = 71^\circ ,\widehat Q = 49^\circ \). Tính số đo góc K của tam giác IHK.
Cho biết \(\Delta ABC = \Delta MNP\), \(AC = 4\)cm, \(\widehat {MPN} = 45^\circ \). Tính độ dài cạnh MP và số đo góc ACB.
Cho \(\Delta ABC = \Delta MNP\) và \(\widehat A + \widehat N = 125^\circ \). Tính số đo góc P.



