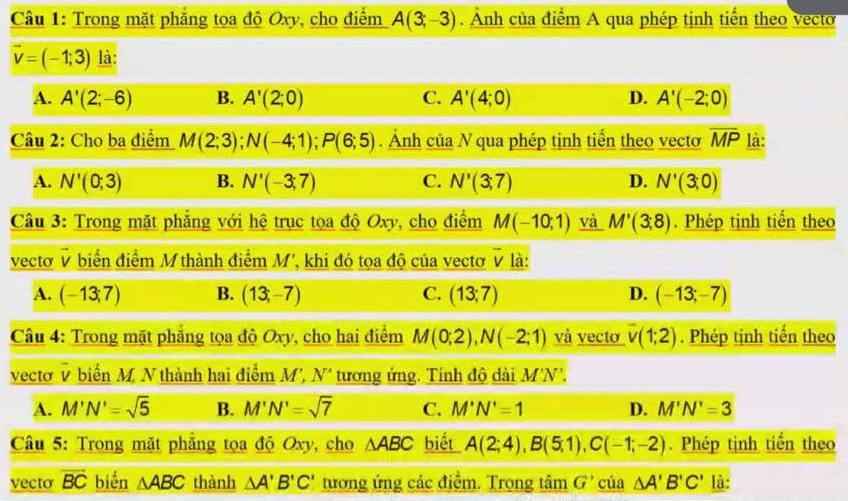
1.
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)





 giúp em với ạ
giúp em với ạ