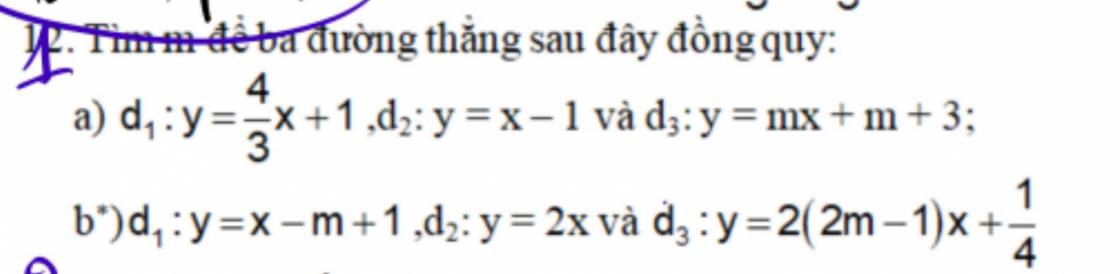a) PT hoành độ giao điểm của \(d_1\)và \(d_2\) là
\(\dfrac{4}{3}x+1=x-1< =>\dfrac{1}{3}x=-2< =>x=-6\)
\(=>y=-6-1=-7\)
Để \(d_1;d_2;d_3\) đồng quy thì \(d_3\) đi qua \(\left(-6;-7\right)=>-7=m.\left(-6\right)+m+3< =>-5m=-10< =>m=2\)
Vậy \(m=2\)
b) PT hoành độ giao điểm của \(d_1\)và \(d_2\) là
\(x-m+1=2x< =>x=1-m=>y=2.\left(1-m\right)=2-2m\)
Để \(d_1;d_2;d_3\) đồng quy thì \(d_3\) đi qua \(\left(1-m;2-2m\right)\)
\(=>2-2m=2\left(2m-1\right)\left(1-m\right)+\dfrac{1}{4}\)
\(< =>2-2m=-4m^2+6m-2+\dfrac{1}{4}\)
\(< =>-4m^2+8m-\dfrac{15}{4}=0\)
\(< =>\dfrac{-1}{4}\left(4m-3\right)\left(5-4m\right)=0\)
\(< =>\left[{}\begin{matrix}4m-3=0\\5-4m=0\end{matrix}\right.< =>\left[{}\begin{matrix}m=\dfrac{3}{4}\\m=\dfrac{5}{4}\end{matrix}\right.\)
Với \(m=\dfrac{3}{4}=>\left\{{}\begin{matrix}\left(d_1\right):y=x+\dfrac{1}{4}\\\left(d_3\right):y=x+\dfrac{1}{4}\end{matrix}\right.=>d_1\equiv d_3\) (loại)
Vậy \(m=\dfrac{5}{4}\)
Bài 2: Đồ thị hàm số y = ax^2 (a khác 0)
Đúng 4
Bình luận (2)
Các câu hỏi tương tự
giúp mình với ạ, cảm ơn

Mọi người giải bài này giúp mình với nha!!!
Cho đường thẳng(d) 2(m-1)x+(m-2)y2
a,Tìm m để (d) cắt (P) tại hai điểm phân biệt A,B với(P) yx2
b,Tìm tọa độ trung điểm I của A,B theo m
c,Tìm m để đường thẳng (d) cách gốc tọa độ một khoảng nhỏ nhất
d,Tìm điểm cố định mà (d) đi qua khi m thay đổi
CẢM ƠN MỌI NGƯỜI NHIỀU Ạ!!!
Đọc tiếp
Mọi người giải bài này giúp mình với nha!!!
Cho đường thẳng(d) 2(m-1)x+(m-2)y=2
a,Tìm m để (d) cắt (P) tại hai điểm phân biệt A,B với(P) y=x2
b,Tìm tọa độ trung điểm I của A,B theo m
c,Tìm m để đường thẳng (d) cách gốc tọa độ một khoảng nhỏ nhất
d,Tìm điểm cố định mà (d) đi qua khi m thay đổi
CẢM ƠN MỌI NGƯỜI NHIỀU Ạ!!!
Cho Parabol (P) y = x2 và đường thẳng d: y = 2mx + 1 :
a) Tìm tọa độ điểm cố định thuộc d khi m thay đổi
b) Tìm m để Parabol (P) cắt d tại 2 điểm phân biệt thỏa mãn: 2mx1 + y2 = x1x2 + 6
Mọi người giúp mình với ạ! Mình cần gấp ạ. Mình cảm ơn !!
a) Vẽ đồ thị hàm số y=2x² (P) b) Bằng phép tính hãy tìm giá trị của m để đường thẳng (d): y= 4x –m tiếp xúc với Parabol (P): y= 2x² Giúp mình vớiiiii
Giúp mình 2 cau nay voi 
giải hộ em bài 2 với bài 3 ạ
Cho đồ thị hàm số y = x^2. Trên đồ thị hàm số lấy điểm M (x0; y0)a, Tìm hệ thức liên hệ giữa x0 và y0b, Kéo dài OM một đoạn MN = OM. Tính tọa độ của điểm N theo x0 và y0c, Tìm quỹ tích điểm N khi M thay đổi trên parabol GIÚP MÌNH VỚI CÁC BẠN ƠI MÌNH ĐANG CẦN GẤP !!!!!!!!CẢM ƠN CÁC BẠN NHIỀU!!!!!!!!!!
Cho đồ thị hàm số y = x^2. Trên đồ thị hàm số lấy điểm M (x0; y0)a, Tìm hệ thức liên hệ giữa x0 và y0b, Kéo dài OM một đoạn MN = OM. Tính tọa độ của điểm N theo x0 và y0c, Tìm quỹ tích điểm N khi M thay đổi trên parabol GIÚP MÌNH VỚI CÁC BẠN ƠI MÌNH ĐANG CẦN GẤP !!!!!!!!CẢM ƠN CÁC BẠN NHIỀU!!!!!!!!!!
a) tìm m để đồ thị hàm số y 3x -4 và y (1-3m )x +m -7 cắt nhau tại một điểm có tung độ bằng hoành độ
b ) cho hpt x+y 5 và 4x +y 2m +9 có nghiệm x;y . Tìm m để biểu thức xy+x -1 đạt max
c ) tìm m để hpt x-2y 1 và 2x + (m-1)y 7m +2 có nghiệm x;y thỏa mãn căn x + căn y 5
d ) tìm m để đường thẳng y(2m -3)x -3m -6 đi qua gốc tọa độ .
Mình đang cần gấp nhờ mọi người giải hộ . Cảm ơn ạ !
Đọc tiếp
a) tìm m để đồ thị hàm số y =3x -4 và y= (1-3m )x +m -7 cắt nhau tại một điểm có tung độ bằng hoành độ
b ) cho hpt x+y =5 và 4x +y = 2m +9 có nghiệm x;y . Tìm m để biểu thức xy+x -1 đạt max
c ) tìm m để hpt x-2y =1 và 2x + (m-1)y = 7m +2 có nghiệm x;y thỏa mãn căn x + căn y = 5
d ) tìm m để đường thẳng y=(2m -3)x -3m -6 đi qua gốc tọa độ .
Mình đang cần gấp nhờ mọi người giải hộ . Cảm ơn ạ !
Giúp em mấy bài này với ạ