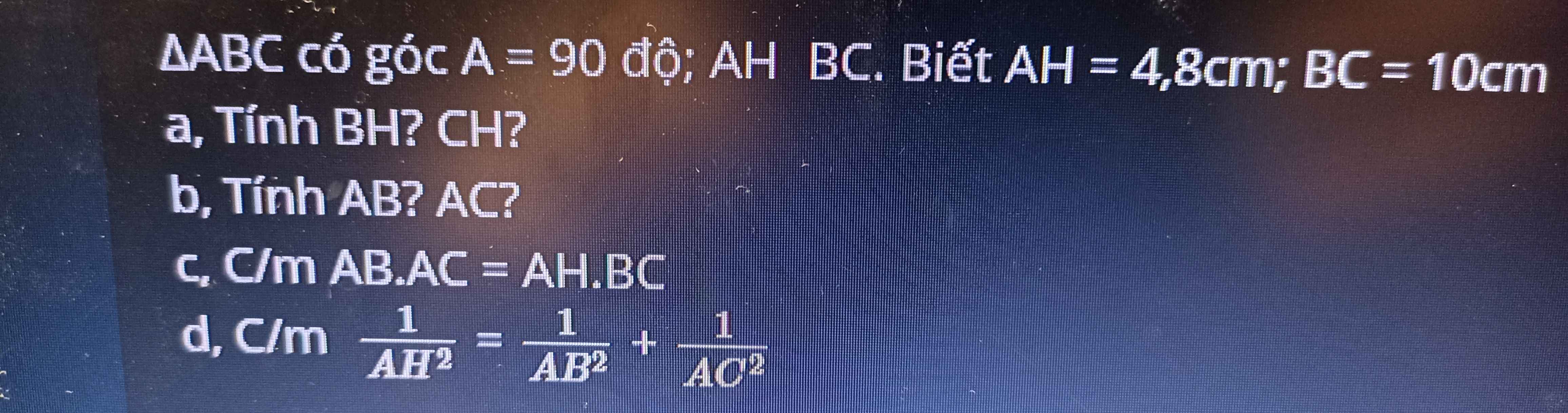
a. Áp dụng hệ thức lượng trong tam giác vuông vào △ABC vuông tại A.
\(AH^2=HB.HC=4,8^2=23,04\)
\(\Rightarrow HB=\dfrac{23,04}{HC}\left(cm\right)\)
Ta có : \(HB+HC=BC=10\left(cm\right)\)
\(\Leftrightarrow\dfrac{23,04}{HC}+HC=10\Rightarrow HC=3,6\left(cm\right)\)
\(\Rightarrow HB=\dfrac{23,04}{3,6}=6,4\left(cm\right)\)
Vậy : HB = 6,4 cm ; HC = 3,6 cm.
b. Áp dụng hệ thức lượng trong tam giác vuông vào △ABC vuông tại A.
1/ \(AB^2=BC.HB\Rightarrow AB=\sqrt{BC.HB}=\sqrt{10.6,4}=8\left(cm\right)\)
2/ \(AC^2=BC.HC\Rightarrow AC=\sqrt{BC.HC}=6\left(cm\right)\)
Vậy : AB = 8 cm ; AC = 6 cm.
c. Ta có : \(AB.AC=6.8=48\)
\(AH.BC=4,8.10=48\)
Vậy : \(AB.AC=AH.BC\left(=48\right)\)
d. Ta có : \(\dfrac{1}{AH^2}=\dfrac{1}{4,8^2}=\dfrac{25}{576}\)
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{8^2}+\dfrac{1}{6^2}=\dfrac{25}{576}\)
Vậy : \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
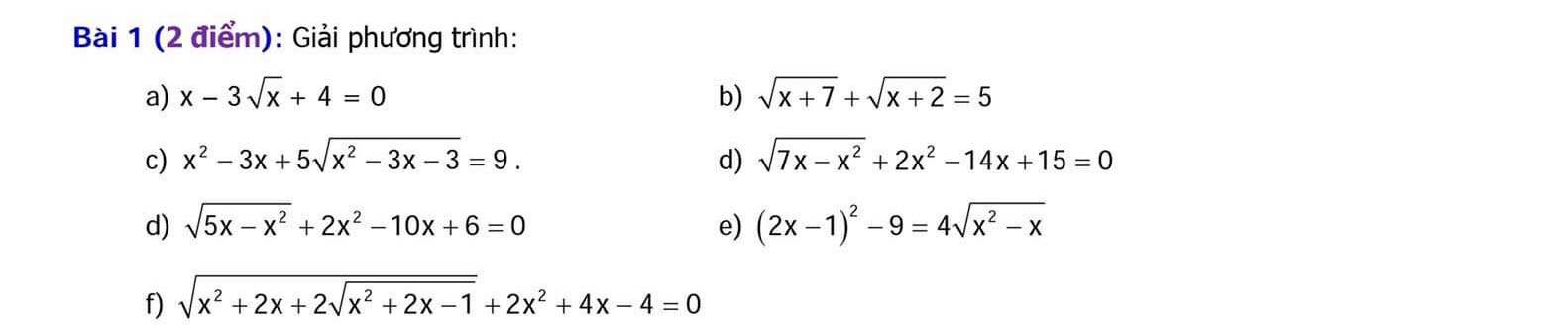
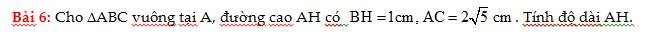giúp mình bài này với ạ
