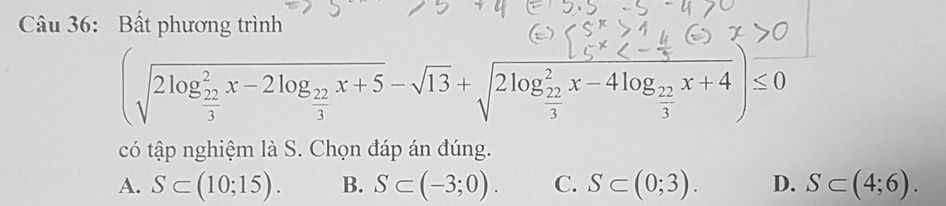ĐKXĐ: \(x>0\)
Đặt \(\log_\frac{22}{3}x=t\) BPT trở thành:
\(\sqrt{2t^2-2t+5}-\sqrt{13}+\sqrt{2t^2-4t+4}\le0\)
\(\Leftrightarrow\sqrt{4t^2-4t+10}+\sqrt{4t^2-8t+8}\le\sqrt{26}\)
\(\Leftrightarrow\sqrt{\left(2t-1\right)^2+9}+\sqrt{\left(2-2t\right)^2+4}\le\sqrt{26}\) (1)
Ta có:
\(\sqrt{\left(2t-1\right)^2+3^2}+\sqrt{\left(2-2t\right)^2+2^2}\ge\sqrt{\left(2t-1+2-2t\right)+\left(3+2\right)^2}=\sqrt{26}\) (2)
(1);(2) \(\Rightarrow\sqrt{\left(2t-1\right)^2+9}+\sqrt{\left(2t-2\right)^2+4}=\sqrt{26}\)
Đẳng thức xảy ra khi và chỉ khi:
\(\dfrac{2t-1}{2-2t}=\dfrac{3}{2}\Rightarrow t=\dfrac{4}{5}\)
\(\Rightarrow \log_\frac{22}{3}x=\dfrac{4}{5}\)
\(\Rightarrow x=\left( \dfrac{22}{3}\right)^\frac{4}{5}\) \(\approx4,923\)
D là đáp án đúng