Xét tam giác ABC như sau: ABC vuông tại A có AD là đường cao.
Ta có: \(AD=\dfrac{AB.AC}{BC}=\dfrac{4.3}{5}=2,4\)
Giả sử đề đúng thì có nghĩa là tồn tại tam giác vuông A'B'C' có độ dài 3 cạnh lần lược là: \(2,4;3;4\) sao cho tam giác này đồng đạng với tam giác ABC.
Mà ta có: \(2,4^2+3^2=14,76< 16=4^2\)
Theo Pitago thì A'B'C' không phải là tam giác vuông. Nên không thể đồng dạng với tam giác ABC được.
Vậy đề sai.
Giả sử tam giác có 3 cạnh lần lược là \(a,b,c\) và có 3 đường cao tương ứng là: \(h_a,h_b,h_c\)
Ta có: \(S_{ABC}=\dfrac{1}{2}.a.h_a=\dfrac{1}{2}.b.h_b=\dfrac{1}{2}.c.h_c\)
\(\Leftrightarrow a.h_a=b.h_b=c.h_c\)
\(\Leftrightarrow\dfrac{a}{\dfrac{1}{h_a}}=\dfrac{b}{\dfrac{1}{h_b}}=\dfrac{c}{\dfrac{1}{h_c}}\)
Vậy tam giác ABC có độ dài các cạnh là \(a,b,c\) sẽ đồng dạng với tam giác A'B'C' có độ dài các cạnh là: \(\dfrac{1}{h_a};\dfrac{1}{h_b};\dfrac{1}{h_c}\) (Điều phải chứng minh).
Giả sử tam giác có 3 cạnh lần lược là a,b,ca,b,c và có 3 đường cao tương ứng là: ha,hb,hcha,hb,hc
Ta có: SABC=12.a.ha=12.b.hb=12.c.hcSABC=12.a.ha=12.b.hb=12.c.hc
⇔a.ha=b.hb=c.hc⇔a.ha=b.hb=c.hc
⇔a1ha=b1hb=c1hc⇔a1ha=b1hb=c1hc
Vậy tam giác ABC có độ dài các cạnh là a,b,ca,b,c sẽ đồng dạng với tam giác A'B'C' có độ dài các cạnh là: 1ha;1hb;1hc1ha;1hb;1hc (Điều phải chứng minh).
Xét tam giác ABC như sau: ABC vuông tại A có AD là đường cao.
Ta có: AD=AB.ACBC=4.35=2,4AD=AB.ACBC=4.35=2,4
Giả sử đề đúng thì có nghĩa là tồn tại tam giác vuông A'B'C' có độ dài 3 cạnh lần lược là: 2,4;3;42,4;3;4 sao cho tam giác này đồng đạng với tam giác ABC.
Mà ta có: 2,42+32=14,76<16=422,42+32=14,76<16=42
Theo Pitago thì A'B'C' không phải là tam giác vuông. Nên không thể đồng dạng với tam giác ABC được.
Vậy đề sai.
a)∆ADB và ∆CDI , ta có :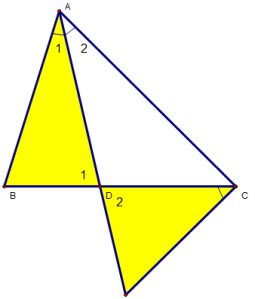
(gt)
(đối đỉnh)
=> ∆ADB ~ ∆CDI
b) )∆ABD và ∆AIC , ta có :
(∆ADB ~ ∆CDI)
(AD là phân giác)
=> ∆ABD ~ ∆AIC
=>
c)=> AD.AI = AB.AC (1)
mà : (∆ADB ~ ∆CDI )
=> AD.DI = BD.CD (2)
từ (1) và (2) :
AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
1. AC2 = CH.BC :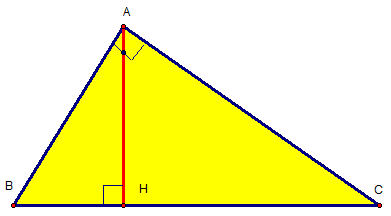
Xét hai ∆ABC và ∆ HAC, ta có :
là góc chung.
=> ∆ABC ~ ∆HAC (g – g)
=>
=> AC2 = CH.BC (1)
Cmtt : AB2 = BH.BC (2)
2. AB2 +AC2 = BC2
Từ (1) và (2), ta có :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
3.AH2 = BH.CH :
Xét hai ∆HBA và ∆ HAC, ta có :
cùng phụ
=> ∆HBA ~ ∆HAC (g – g)
=>
=> AH2 = BH.CH
4. AH.BC = AB.AC :
Ta có : (∆ABC ~ ∆HAC)
=> AH.BC = AB.AC.
a) xét ∆ABD và ∆AEG, ta có :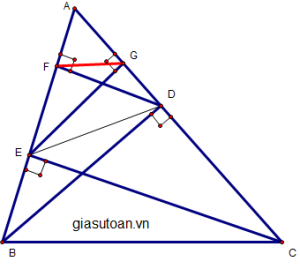
BD AC (BD là đường cao)
EG AC (EG là đường cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
b) =>
=> AD.AE = AB.AG (1)
cmtt, ta được : AD.AE = AC.AF (2)
từ (1) và (2) suy ra :
AD.AE = AB.AG = AC.AF
c) xét ∆ABC, ta có :
AB.AG = AC.AF (cmt)
=> FG // BC (định lí đảo talet)
a)xét ∆HBE và ∆HCD, ta có :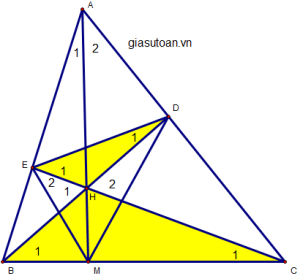
(gt)
(đối đỉnh)
=> ∆HBE ~ ∆HCD (g – g)
b) ∆HED và ∆HBC, ta có :
(∆HBE ~ ∆HCD)
=>
(đối đỉnh)
=> ∆HED ~ ∆HBC (c – g – c)
=> (1)
mà : đường cao BD và CE cắt nhau tại H (gt)
=> H là trực tâm.
=> AH BC tại M.
=>
mặt khác :
=> (2)
từ (1) và (2) :
hay :
c) cmtt câu b, ta được : (3)
xét ∆BCD, ta có :
DB = DC (gt)
=> ∆BCD cân tại D
=>
mà : (∆HED ~ ∆HBC)
=>
mà :
(cmt)
=>
hay :
=> ED EM.


















