a)
Ta có : AC = BD (GT)
Mà OA = OB (GT)
=> OC = OD
Xét \(\Delta AOD\) = \(\Delta BOC\) có :
OA = OB (GT)
OC = OD (C/M trên)
\(\widehat{AOD}\) = \(\widehat{BOC}\) ( 2 góc đối đỉnh )
=> \(\Delta AOD\) = \(\Delta BOC\) (c.g.c)
=> AD = BC ( 2 cạnh tương ứng )
b)
Vì \(\Delta AOD\) = \(\Delta BOC\) (câu a)
\(\widehat{CBO}\) = \(\widehat{DAO}\) ( 2 góc tương ứng )
Ta có :
\(\widehat{CBO}\) + \(\widehat{OBE}\) = \(180^o\) ( 2 góc kề bù )
\(\widehat{DAO}\) + \(\widehat{OAE}\) = \(180^o\) ( 2 góc kề bù )
Mà \(\widehat{CBO}\) = \(\widehat{DAO}\)
=> \(\widehat{EAC}\) = \(\widehat{EBD}\) (ĐPCM)
c)






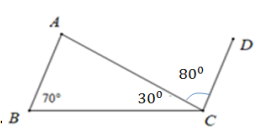



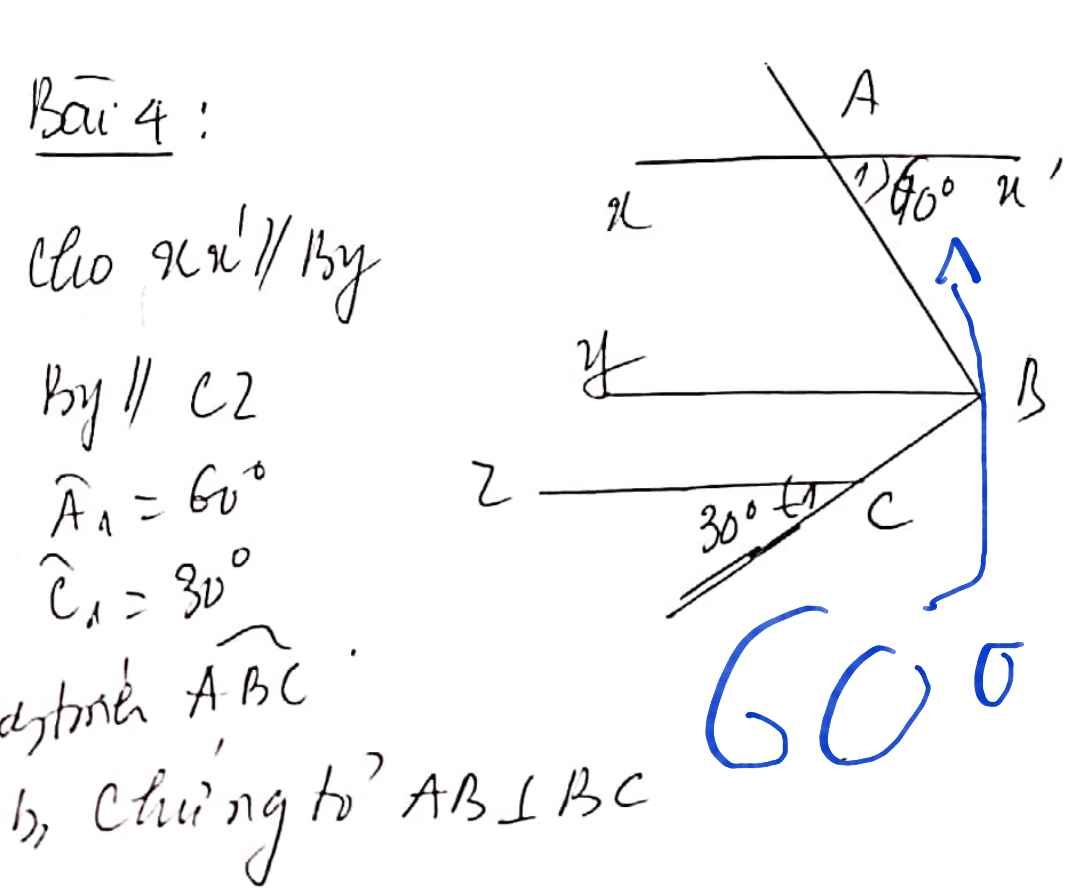
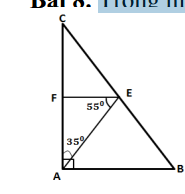

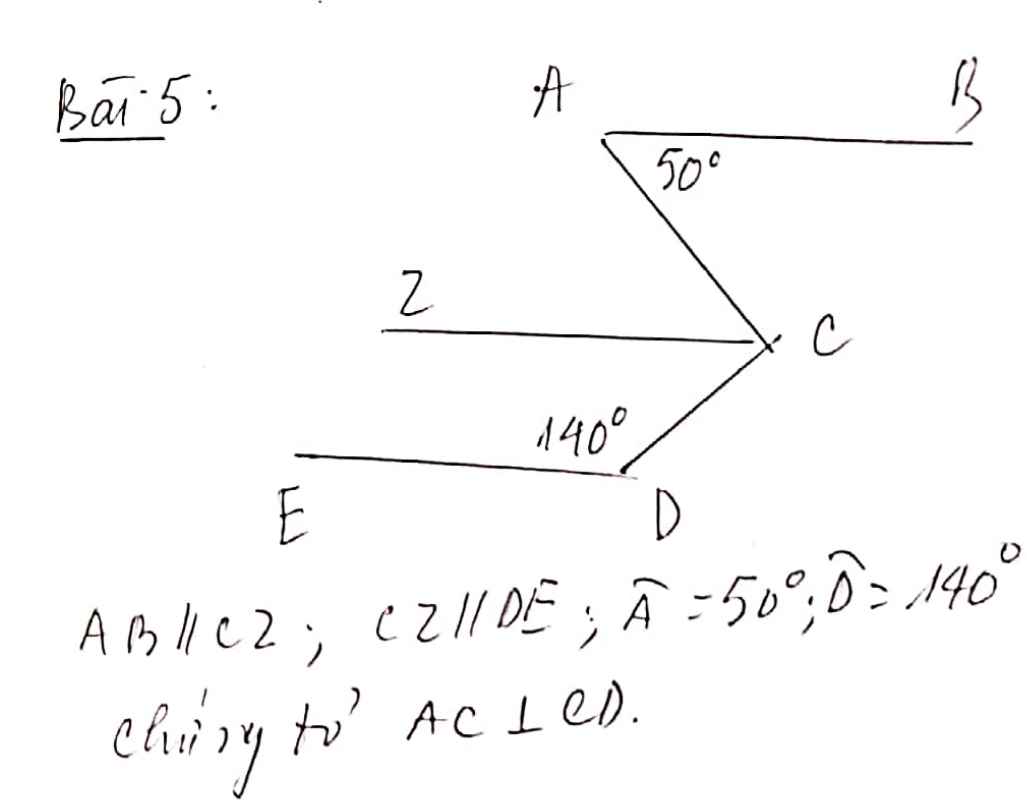

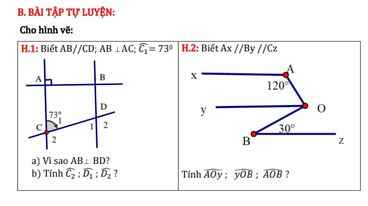 giúp mik giải bài toán hình 7 này với ạ
giúp mik giải bài toán hình 7 này với ạ

