Gọi vận tốc ca nô là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{36}{x+6}+\dfrac{36}{x-6}=\dfrac{9}{2}\Rightarrow x=18\)
Vậy ...
Gọi vận tốc ca nô là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{36}{x+6}+\dfrac{36}{x-6}=\dfrac{9}{2}\Rightarrow x=18\)
Vậy ...
cho t.giác abc vuông tại a,ab=15cm,ac=20cmtrên cạch bc lấy điiểm h sao cho bh=9cm a)c.minh t.giác ahb đ.dạng với t.giác cab,và ab*ca=cb*ah b)tính độ dài các đoạn thẳng AH và chứng minh AH vuông góc BC c)kẻ HK vuông góc AB và HQ vuông góc AC tính chu vi tứ giác AKHQ
cho tam giác ABC có độ dài 3 cạnh a,b,c thỏa mãn
\(\dfrac{ab}{b+c}+\dfrac{bc}{c+a}+\dfrac{ca}{a+b}=\dfrac{ab}{c+a}+\dfrac{bc}{a+b}+\dfrac{ca}{b+c}\)
cm: tam giác ABC cân
1)Tam giác ABC có AB = 13cm BC = 15cm và CA= 17cm. Tam giác A'B'C'đồng dạng với tam giác ABC có cạnh nhỏ nhất là 6,5 .Tính độ dài các cạnh còn lại của tam giác A'B'C '
2) Cho tam giác ABC có độ dài các cạnh AB = 21,5 cm BC = 25,3 cm BC = 30,7 cm .Tính độ dài các cạnh của tam A'B'C'đồng dạng với tam giác abc trong các trường hợp sau:
a) A'B' lớn hơn AB 6 cm
b) A'B' nhỏ hơn AC 10,5 cm (Hãy tính chính xác đến hai chữ số ở phần thập phân)
Cho tam giác ABC có cạch BC = 10cm, CA = 14cm , AB = 6cm. Tam giác ABC đồng dạng với tam giác DEF có cạch nhỏ nhất là 9cm. Tính các cạch còn lại của tam giác DEF
Mn giúp ạ
Tam giác ABC có AB = 3cm, BC = 5cm và CA = 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5 cm.
Tính các cạnh còn lại của tam giác A'B'C' ?
Cho tam giác ABC có AB = 16,2 cm, BC = 24,3 cm; AC = 32,7 cm. Tính độ dài các cạnh của tam giác A'B'C', biết rằng A'B'C' đồng dạng với tam giác ABC và
a) A'B' lớn hơn cạnh AB là 10,8 cm
b) A'B' bé hơn cạnh AB là 5,4 cm
TAM GIÁC ABC CÓ AB=3cm, BC=5cm, CA=7cm
TAM GIÁC A'B'C' ĐỒNG DẠNG VỚI TAM GIÁC ABC THEO TỈ SỐ ĐỒNG DẠNG 5/2. TÍNH ĐỘ DÀI CÁC CẠNH CỦA TAM GIÁC A'B'C'
cho tam giác ABC nhọn. Trên tia đối của tia BA lấy điểm D sao cho 2BD=BA. Trên tia đối của tia CA lấy điểm E sao cho 2CE=CA. Chứng minh tam giác ABC đồng dạng với tam giác ADE
Hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC (h.21).
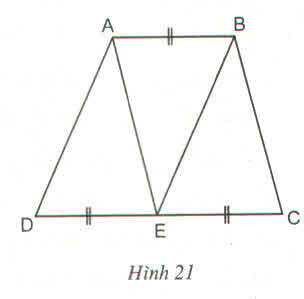
Chứng minh rằng 3 tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)