\(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{6x-9}-\sqrt[3]{27x-54}}{\left(x-3\right)\left(x^2+3x-18\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\sqrt{6x-9}-x+x-\sqrt[3]{27x-54}}{\left(x-3\right)^2\left(x+6\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\dfrac{6x-9-x^2}{\sqrt{6x-9}+x}+\dfrac{x^3-27x+54}{x^2+x\cdot\sqrt[3]{27x-54}+\sqrt[3]{\left(27x-54\right)^2}}}{\left(x-3\right)^2\left(x+6\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\dfrac{-\left(x-3\right)^2}{\sqrt{6x-9}+x}+\dfrac{\left(x-3\right)^2\left(x+6\right)}{x^2+x\cdot\sqrt[3]{27x-54}+\sqrt[3]{\left(27x-54\right)^2}}}{\left(x-3\right)^2\left(x+6\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\dfrac{-1}{\sqrt{6x-9}+x}+\dfrac{\left(x+6\right)}{x^2+x\cdot\sqrt[3]{27x-54}+\sqrt[3]{\left(27x-54\right)^2}}}{\left(x+6\right)}\)
\(=\dfrac{-\dfrac{1}{\sqrt{6\cdot3-9}+3}+\dfrac{3+6}{3^2+3\cdot\sqrt[3]{27\cdot3-54}+\sqrt[3]{\left(27\cdot3-54\right)^2}}}{3+6}\)
\(=\dfrac{-\dfrac{1}{3+3}+\dfrac{9}{9+3\cdot3+3^2}}{9}=\dfrac{-\dfrac{1}{6}+\dfrac{1}{3}}{9}=\dfrac{\dfrac{1}{6}}{9}=\dfrac{1}{54}\)
Phương pháp đạo hàm ý em là định lý L'Hopital hả? Định lý L'Hopital là 1 phương pháp rất mạnh để giải các bài giới hạn dạng phân thức \(\dfrac{0}{0}\) hoặc \(\dfrac{\infty}{\infty}\), nhưng người ta hạn chế sử dụng khi xuất hiện căn thức (lý do là khi đạo hàm thì căn thức không những gọn đi mà còn "phình to" ra rất nhiều). Ưu điểm là nó khử dạng vô định rất nhanh chóng. Còn khi phân thức mà tử mẫu đều ko xuất hiện căn thức thì đó đúng là 1 pp mạnh tuyệt đối.
Định lý nó như sau: nếu \(f\left(x\right)\) và \(g\left(x\right)\) cùng tiến tới 0 (hoặc \(+\infty\) hoặc \(-\infty\)) khi \(x\rightarrow a\) nào đó thì:
\(\lim\limits_{x\rightarrow a}\dfrac{f\left(x\right)}{g\left(x\right)}=\lim\limits_{x\rightarrow a}\dfrac{f'\left(x\right)}{g'\left(x\right)}\)
Bài này có cả căn bậc 3 nên đạo hàm ko được đẹp lắm. Tự hiểu là giới hạn nha, vì công thức latex gõ giới hạn hơi phức tạp, tốn thời gian lắm, gõ 1 biểu thức thôi thì lẹ gấp chục lần:
\(\dfrac{\sqrt[]{6x-9}-\sqrt[3]{27x-54}}{\left(x-3\right)\left(x^2+3x-18\right)}=\dfrac{\dfrac{3}{\sqrt[]{6x-9}}-\dfrac{1}{\sqrt[3]{\left(x-2\right)^2}}}{x^2+3x-18+\left(x-3\right)\left(2x+3\right)}\)
Vậy là mất dạng vô định, thay số là xong.
Còn thêm bớt liên hợp thì khá đơn giản, do \(x\rightarrow3\) nên ta thay \(x=3\) vào 1 căn thức bất kì, ví dụ căn đầu, được \(\sqrt{6.3-9}=3\), vậy ta chỉ cần thêm bớt 3 vào tử số rồi liên hợp là được:
\(=\dfrac{\left(\sqrt[]{6x-9}-3\right)+\left(3-3\sqrt[3]{x-2}\right)}{\left(x-3\right)\left(x^2+3x-18\right)}\)
Ủa ko để ý tới pt \(x^2+3x-18=0\) còn có nghiệm \(x=3\) do ko tính toán :D
Vậy nghĩa là mẫu xuất hiện nghiệm kép, với dạng mẫu xuất hiện nghiệm kép thì ta cần liên hợp tử cũng phải xuất hiện nghiệm kép. Có 2 cách thực hiện: dùng máy tính và dùng tay.
Biểu thức liên hợp cần thêm vào phải là 1 hàm bậc nhất dạng \(ax+b\)
Theo quy tắc tiếp tuyến (của lớp 12), ta có \(a=\left(\sqrt{6x-9}\right)'_{x=3}\)
Hay trong máy tính thì bấm 
, kết quả được 1
Vậy \(a=1\) (dùng tay thì đạo hàm biểu thức \(\left(\sqrt{6x-9}\right)'=\dfrac{3}{\sqrt{6x-9}}\) rồi thay x=3 cũng được 1)
Khi đó ta liên hợp: \(\sqrt{6x-9}-\left(x+b\right)\)
Liên hợp trên phải có nghiệm \(x=3\), tức là thay 3 vào thì nó =0
\(\Rightarrow\sqrt{6.3-9}-\left(3+b\right)=0\)
\(\Rightarrow b=0\)
Vậy biểu thức cần thêm bớt là \(1.x+0=x\), hay tử số ta cần phân tích thành:
\(\left(\sqrt[]{6x-9}-x\right)+\left(x-3\sqrt[3]{x-2}\right)\)
Gặp dạng giới hạn \(x\rightarrow a\) mà mẫu số phân tích xuất hiện \(\left(x-a\right)^2\) thì cứ làm như vậy là được
Hình như em hiểu nhầm 1 số chỗ, vậy nói lại xíu cho rõ nha
Bài toán tính giới hạn khi \(x\rightarrow x_0\) mà tử số có căn và mẫu thức có bình phương dạng \(\left(x-x_0\right)^2\) (kiểu bài này)
Trước hết, ta chỉ cần để ý tới căn bậc 2 trên tử, ở bài này là \(\sqrt{6x-9}\)
Ta cần thêm bớt biểu thức liên hợp với nó dạng \(ax+b\) với a;b là các số thực (sẽ tìm sau).
Quy tắc tìm a;b như sau:
Tính đạo hàm của căn thức tại \(x=x_0\), tức là tính đạo hàm của \(\sqrt{6x+9}\) tại \(x=3\). Kết quả ra bao nhiêu chính là hệ số a của \(ax+b\)
Ví dụ bài này ta tính đạo hàm \(\sqrt{6x+9}\) tại \(x_0=3\) ta được kết quả \(=1\), vậy \(a=1\)
Sau đó thay \(x_0\) (ở bài này là \(x_0=3\)) và a vào \(\sqrt{6x+9}-\left(ax+b\right)=0\) là tính được b
Ko hiểu đoạn kia trình bày thế nào mà em hiểu nhầm ở đâu nhỉ? Thấy quy tắc tính rất đơn giản mà, bấm máy \(\dfrac{d}{dx}\left(\text{căn thức}\right)_{x=x_0}\) (với \(x\rightarrow x_0\)) sẽ được a, thay a và \(x_0\) vào \(\text{căn thức}-\left(ax+b\right)=0\) sẽ được b, vậy là tìm được biểu thức liên hợp thôi.
Ko tìm được đề nào khác dạng này để thử, thôi lấy ví dụ vậy, tính giới hạn: \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
Mẫu có nghiệm kép \(x=0\) nên nếu chỉ thêm bớt 1 vào tử số để liên hợp sẽ ko khử hết được, cần sử dụng pp vừa nãy:
Đầu tiên ta cần liên hợp: \(\sqrt[]{4x+1}-\left(ax+b\right)\) (1)
Để tìm a, ta bấm máy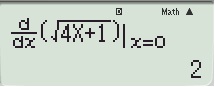 
(giới hạn \(x\rightarrow x_0\) thì \(\dfrac{d}{dx}\left(\text{căn thức}\right)_{x=x_0}\) , ví dụ bài này \(x_0=0\))
Vậy ta được \(a=2\)
Thay vào a vào (1) : \(\sqrt{4x+1}-\left(2x+b\right)=0\)
Pt (1) phải có nghiệm \(x=x_0\) hay ở đây là \(x=0\)
\(\Rightarrow\sqrt{4.0+1}-\left(2.0+b\right)=0\Rightarrow b=1\)
Vậy a=2, b=1 hay ta cần liên hợp: \(\sqrt{4x+1}-\left(2x+1\right)\)
Vậy bài toán được giải như sau:
\(...=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt[]{4x+1}-\left(2x+1\right)\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{4x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
Như vậy là khử được hết bình phương chỉ cần thay số tính
