a: 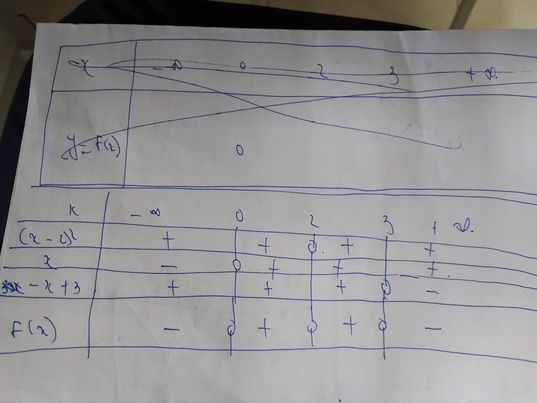
b: 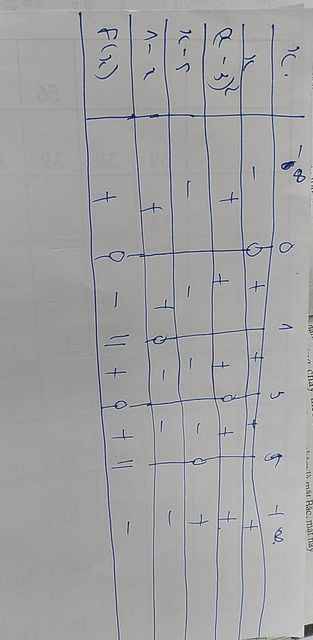
c: Đặt f(x)=0
=>-x^2+x+6=0
=>x^2-x-6=0
=>x=3 hoặc x=-2
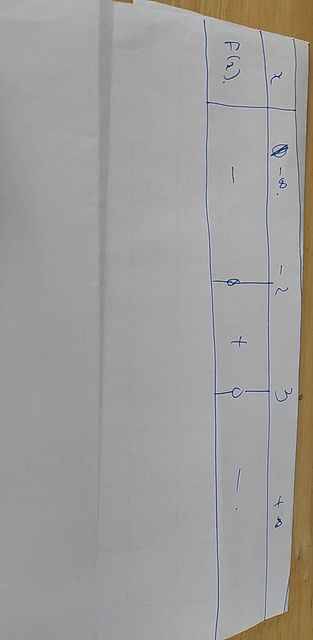
d: 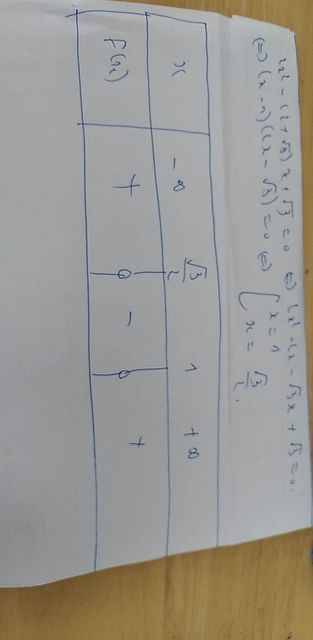
a: 
b: 
c: Đặt f(x)=0
=>-x^2+x+6=0
=>x^2-x-6=0
=>x=3 hoặc x=-2

d: 
Xét dấu các biểu thức :
a. \(f\left(x\right)=\left(2x-1\right)\left(x+3\right)\)
b. \(f\left(x\right)=\left(-3x-3\right)\left(x+2\right)\left(x+3\right)\)
c. \(f\left(x\right)=-\dfrac{4}{3x+1}-\dfrac{3}{2-x}\)
d. \(f\left(x\right)=4x^2-1\)
lập bảng xét dấu của
a) f(x)=\(\frac{2x+6}{5x-10}\)
b) f(x)=(2x-4)*(-x+1)
c) f(x)=\(\frac{\left(x+3\right)\cdot\left(x-6\right)}{x\cdot\left(x+2\right)\cdot\left(-x-3\right)}\)
Xét dấu các biểu thức sau :
\(f\left(x\right)=\left(-2x+3\right)\left(x-2\right)\left(x+4\right)\)
Bài 1: xét dấu các biểu thức sau: (giải chi tiết, cặn kẽ giúp mình nhe)
a)\(f\left(x\right)\frac{1}{3-x}-\frac{1}{3+x}\)
b)\(f\left(x\right)=2x^2+2x+5\)
c)\(f\left(x\right)=\left(2x-1\right)\left(x^2-4\right)\)
d)\(f\left(x\right)=\frac{4x^2-19x+12}{x-7}\)
Xét dấu biểu thức sau đây:\(f\left(x\right)=\) \(\dfrac{2x+3}{x+1}+\dfrac{x+6}{-3x-2}\)
Xét dấu các biểu thức sau :
\(f\left(x\right)=\dfrac{2x+1}{\left(x-1\right)\left(x+2\right)}\)
bài 1: xét dấu các nhị thức sau:
a) f(x)=3x+4
b) g(x)=4x-5
c) h(x)=-5x+10
d) k(x)=-6x-18
e) l(x)=2018-2x
bài 2: xét dấu các biểu thức sau:
a) f(x) =(2x-4)(3x+5)
b) g(x)=(-2x+8)(x-9)
c) h(x)=(-\(\frac{x}{3}\)-2)(1-2x)
d) k(x)=(1-2x)(x+1)(x-1)
e) l(x)=\(\frac{x-1}{x+1}\)
f) m(x)=\(\frac{4-2x}{3+x}\)
g) n(x)=\(\frac{\left(1-2x\right)\left(2x-1\right)}{3+x}\)
h) p(x)=\(\frac{x\left(x-1\right)\left(x+2\right)}{2-3x}\)
i) q(x)=\(\frac{\left(x-1\right)\left(2x-7\right)}{\left(2+x\right)^2}\)
1. Giải các bất phương trình sau :
a, \(\left|3x-7\right|\ge-2x+28\)
b, \(\left|x^2+x-3\right|>x^2+3x+3\)
c, \(\left|x-1\right|+\left|-2x+6\right|\ge x-5\)
d, \(\frac{\left|x-2\right|+7}{\left|4-x\right|+x+1}< 2\)
e, \(\frac{\left|2x-1\right|}{\left(x+1\right)\left(x-2\right)}\le\frac{1}{2}\)
f, \(\frac{\left(2x-3\right)\left(\left|x-1\right|+2\right)}{\left|x-1\right|-2}\le0\)
Xét dấu các biểu thức sau :
\(f\left(x\right)=\left(4x-1\right)\left(x+2\right)\left(3x-5\right)\left(-2x+7\right)\)