Kiểm tra bằng thước đo góc, ta được: \(\widehat {xOC} = \widehat {yOC}\)
Bài 2. Tia phân giác của một góc
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Kiểm tra lại bằng thước đo góc để thấy góc mIK và nIK trong Hoạt động 3 là bằng nhau.
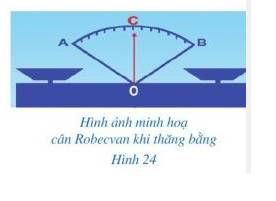
Hình 24 gợi nên hình ảnh tia OC nằm trong góc AOB và chia góc đó thành hai góc bằng nhau là AOC và BOC.
Tia OC được gọi là tia gì của góc AOB?
Cho \(\widehat {xOy} = 120^\circ \). Vẽ tia phân giác của góc xOy bằng 2 cách:
a) Sử dụng thước thẳng và compa; b) Sử dụng thước hai lề
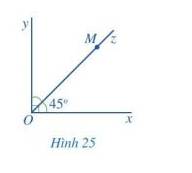
Quan sát góc vuông xOy và tia Oz ở Hình 25.
a) Mỗi điểm M (M khác O) thuộc tia Oz có phải là điểm trong của góc xOy hay không? Tia Oz có nằm trong góc xOy hay không?
b) Tính số đo góc yOz.
c) So sánh hai góc xOz và yOz.
Ở Hình 31 có góc vuông xOy, các tia On, Oz, Om nằm trong góc đó và \(\widehat {xOn} = \widehat {nOz},\widehat {yOm} = \widehat {mOz}\).
a) Các tia Om, On có tương ứng là tia phân giác của góc yOz và xOz hay không?
b) Cho biết số đo góc mOn.

Để xác định phương hướng trên bản đồ hay trên thực địa, người ta thường xác định 8 hướng ( Bắc, Nam, Đông, Tây, Đông Bắc, Đông Nam, Tây Nam, Tây Bắc) như Hình 29. Trong đó:

a) Tia OB là tia phân giác của những góc nào?
b) Tia OT là tia phân giác của những góc nào?
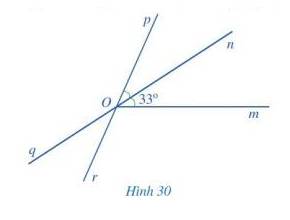
Trong Hình 30, tính số đo của \(\widehat {mOp};\widehat {qOr};\widehat {pOq}\)