a) 1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ 1 \right\}\)
2. Sự biến thiên:
Ta có: \(y = \frac{{2{x^2} - x + 4}}{{x - 1}} = 2x + 1 + \frac{5}{{x - 1}}\)
\(y' = 2 - \frac{5}{{{{\left( {x - 1} \right)}^2}}},y' = 0 \Leftrightarrow x = \frac{{2 - \sqrt {10} }}{2}\) hoặc \(x = \frac{{2 + \sqrt {10} }}{2}\)
Trong khoảng \(\left( { - \infty ;\frac{{2 - \sqrt {10} }}{2}} \right)\) và \(\left( {\frac{{2 + \sqrt {10} }}{2}; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Trong khoảng \(\left( {\frac{{2 - \sqrt {10} }}{2};1} \right)\) và \(\left( {1;\frac{{2 + \sqrt {10} }}{2}} \right)\), \(y' < 0\) nên hàm số nghịch biến.
Hàm số đạt cực đại tại \(x = \frac{{2 - \sqrt {10} }}{2}\), giá trị cực đại .
Hàm số đạt cực tiểu tại \(x = \frac{{2 + \sqrt {10} }}{2}\), giá trị cực đại \({y_{CT}} = 2\sqrt {10} + 3\).
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - x + 4}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} - x + 4}}{{x - 1}} = - \infty \)
\(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{2{x^2} - x + 4}}{{x - 1}} = - \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2{x^2} - x + 4}}{{x - 1}} = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( {2x + 1 + \frac{5}{{x - 1}} - \left( {2x + 1} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{5}{{x - 1}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {2x + 1 + \frac{5}{{x - 1}} - \left( {2x + 1} \right)} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{5}{{x - 1}} = 0\)
Do đó, đồ thị hàm số nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = 2x + 1\) làm tiệm cận xiên.
Bảng biến thiên:
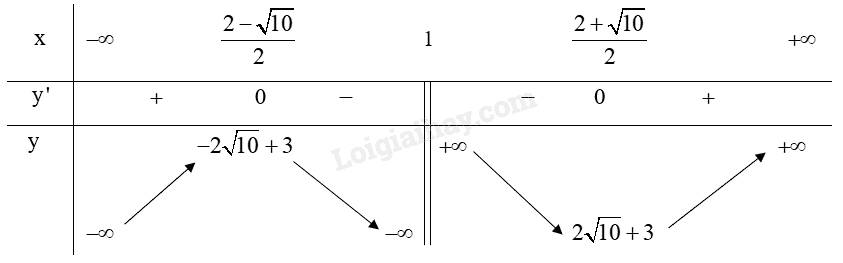
3. Đồ thị:
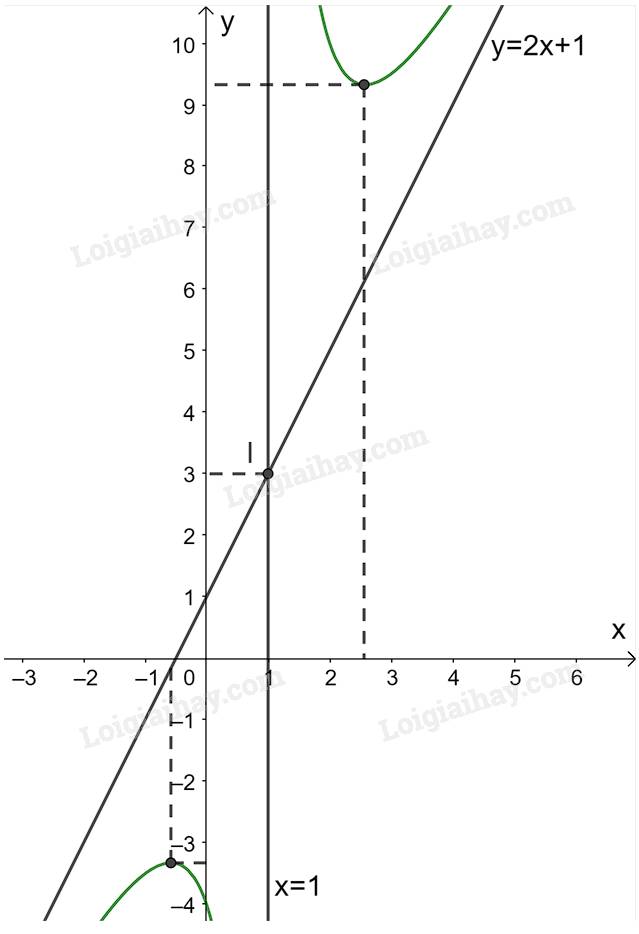
Giao điểm của đồ thị hàm số với trục tung là (0; -4).
Đồ thị hàm số không cắt trục Ox.
Đồ thị hàm số nhận giao điểm I(1; 3) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
b) \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}}\)
1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ { - 3} \right\}\)
2. Sự biến thiên:
Ta có: \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}} = x - 1 + \frac{4}{{x + 3}}\)
\(y' = 1 - \frac{4}{{{{\left( {x + 3} \right)}^2}}},y' = 0 \Leftrightarrow x = - 1\) hoặc \(x = - 5\).
Trong khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 1; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Trong khoảng \(\left( { - 5; - 3} \right)\) và \(\left( { - 3; - 1} \right)\), \(y' < 0\) nên hàm số nghịch biến.
Hàm số đạt cực đại tại \(x = - 5\), giá trị cực đại .
Hàm số đạt cực tiểu tại \(x = - 1\), giá trị cực tiểu \({y_{CT}} = 0\).
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 2x + 1}}{{x + 3}} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 2x + 1}}{{x + 3}} = - \infty \)
\(\mathop {\lim }\limits_{x \to - {3^ - }} y = \mathop {\lim }\limits_{x \to - {3^ - }} \frac{{{x^2} + 2x + 1}}{{x + 3}} = - \infty ;\mathop {\lim }\limits_{x \to - {3^ + }} y = \mathop {\lim }\limits_{x \to - {3^ + }} \frac{{{x^2} + 2x + 1}}{{x + 3}} = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( {x - 1 + \frac{4}{{x + 3}} - \left( {x - 1} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{{x + 3}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {x - 1 + \frac{4}{{x + 3}} - \left( {x - 1} \right)} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{4}{{x + 3}} = 0\)
Do đó, đồ thị hàm số nhận đường thẳng \(x = - 3\) làm tiệm cận đứng và đường thẳng \(y = x - 1\) làm tiệm cận xiên.
Bảng biến thiên:
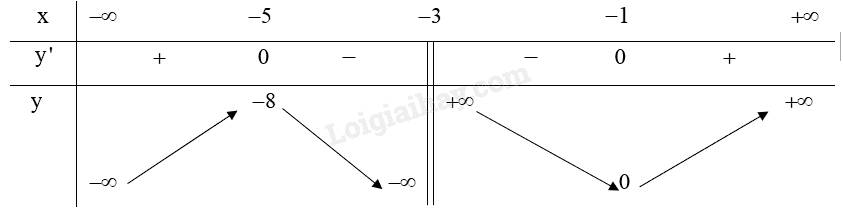
3. Đồ thị:
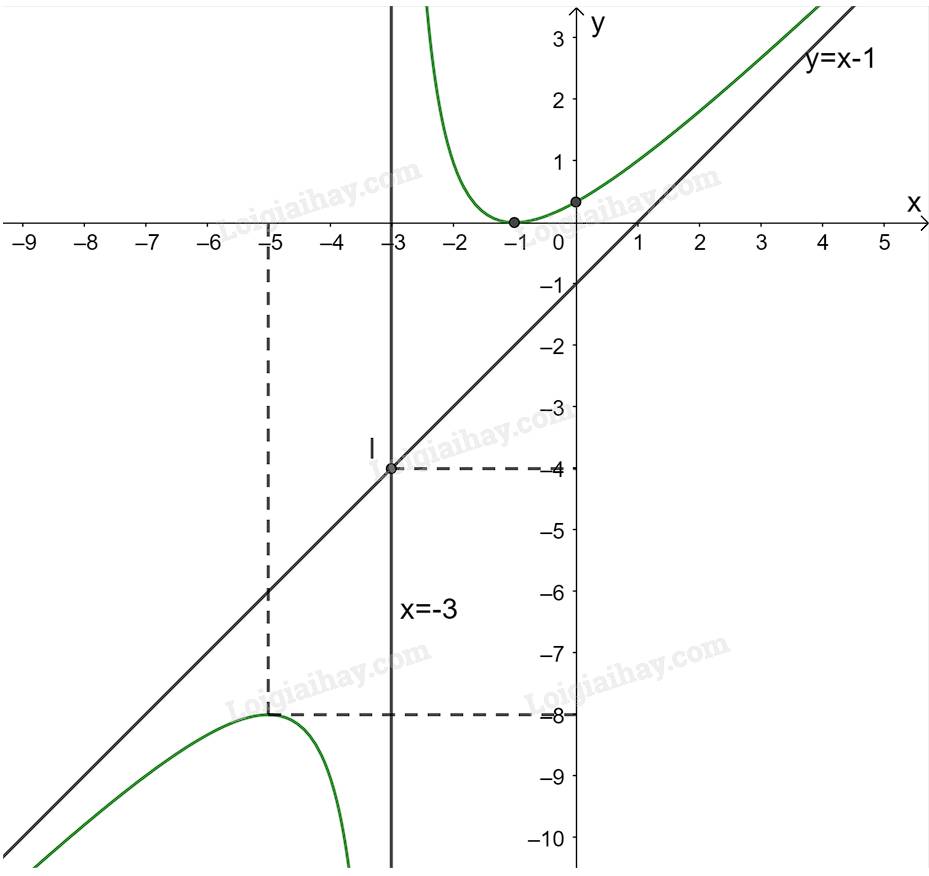
Giao điểmcủa đồ thị hàm số với trục tung là \(\left( {0;\frac{1}{3}} \right)\).
\(y = 0 \Leftrightarrow \frac{{{x^2} + 2x + 1}}{{x + 3}} = 0 \Leftrightarrow x = - 1\)
Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 1;0} \right)\).
Đồ thị hàm số nhận giao điểm \(I\left( { - 3; - 4} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.




