Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)
Bài 3. Hàm số lượng giác và đồ thị
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Hàm số \(y = \sin x\) đồng biến hay nghịch biến trên khoảng \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right)\)
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
Với mỗi số thực m, tìm số giao điểm của đường thẳng y=m với đồ thị hàm số \(y = \tan x\)trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
a) Hàm số y = tanx nhận giá trị bằng – 1
b) Hàm số y = tanx nhận giá trị bằng 0
c) Hàm số y = cotx nhận giá trị bằng 1
d) Hàm số y = cotx nhận giá trị bằng 0
Cho hàm số y cos xa) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm left( {x;cos x} right) với x in left[ { - pi ;pi } right] và nối lại ta được đồ thị hàmsố y cos x trên đoạn x in left[ { - pi ;pi } right] (Hình 27)c) Làm tương tự như trên đối với các đoạn left[ { - 3pi ; - pi } right], left[ {pi ;3pi } right],...ta có đồ thị hàm số y cos xtrên R đư...
Đọc tiếp
Cho hàm số \(y = \cos x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm
số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
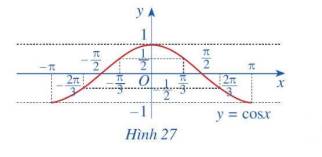
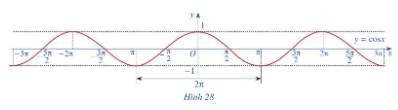
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.
Dùng đồ thị hàm số, hãy cho biết:a) Với mỗi m in left[ { - 1;1} right], có bao nhiêu giá trị alpha in left[ { - frac{pi }{2};frac{pi }{2}} right] sao cho sin alpha mb) Với mỗi m in left[ { - 1;1} right], có bao nhiêu giá trị alpha in left[ {0;pi } right] sao cho cos alpha mc) Với mỗi m in mathbb{R}, có bao nhiêu giá trị alpha in left[ { - frac{pi }{2};frac{pi }{2}} right] sao cho tan alpha md) Với mỗi m in mathbb{R}, có bao nhiêu giá trị alpha in left[ {0;pi } right] sa...
Đọc tiếp
Dùng đồ thị hàm số, hãy cho biết:
a) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)
Xét tập hợp \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |\,k \in \mathbb{Z}} \right\}\). Với mỗi số thực \(x \in D\), hãy nêu định nghĩa \(\tan x\)
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) để:
a) Hàm số y = sinx nhận giá trị bằng 1
b) Hàm số y = sinx nhận giá trị bằng 0
c) Hàm số y = cosx nhận giá trị bằng – 1
d) Hàm số y = cosx nhận giá trị bằng 0
Với mỗi số thực m, tìm số giao điểm của đường thẳng y=m với đồ thị hàm số \(y = \cot x\)trên khoảng \(\left( {0;\pi } \right)\)


