Hàm số ở câu a) \(y = 2{x^2} - 6\) là hàm số bậc hai với \(a = 2,b = - 6,c = 0\)
Hàm số ở câu c) \(y = - 5{x^2} + 15x + 20\) là hàm số bậc hai với \(a = - 5,b = 15,c = 20\)
Hàm số ở câu b) không phải là hàm số bậc hai.
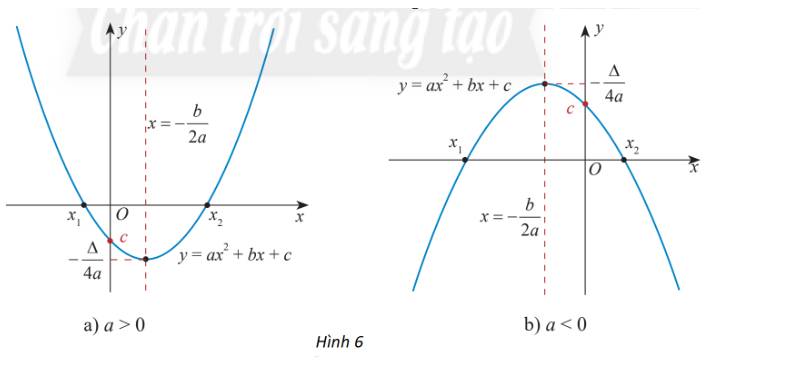
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.
Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?
a) \(y = 2x(x - 3)\)
b) \(y = x({x^2} + 2) - 5\)
c) \(y = - 5(x + 1)(x - 4)\)
Hàm số nào sau đây là hàm số bậc hai?
a) \(y = 9{x^2} + 5x + 4\)
b) \(y = 3{x^3} + 2x + 1\)
c) \(y = - 4{(x + 2)^3} + 2(2{x^3} + 1) + x + 4\)
d) \(y = 5{x^2} + \sqrt x + 2\)
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:
a) \(y = m{x^4} + (m + 1){x^2} + x + 3\)
b) \(y = (m - 2){x^3} + (m - 1){x^2} + 5\)
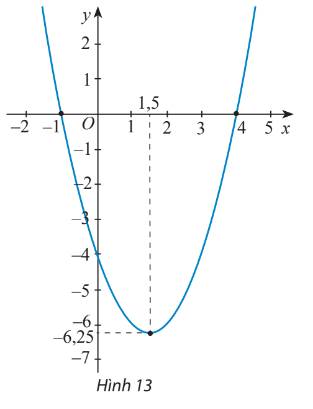
Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.
Vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\) rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.
Cho hàm số \(y = 2{x^2} + x + m\). Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.
Tìm khoảng đồng biến, khoảng nghịch biến của hàm số \(y = 2{x^2} - 6x + 11.\) Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?
