Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai.
Bài 16: Hàm số bậc hai
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
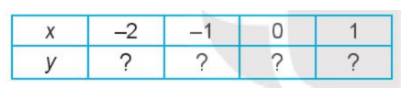
Cho hàm số \(y = (x - 1)(2 - 3x)\)
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho.
Vẽ các đường parabol sau:
a) \(y = {x^2} - 3x + 2\)
b) \(y = - 2{x^2} + 2x + 3\)
c) \(y = {x^2} + 2x + 1\)
d) \(y = - {x^2} + x - 1\)
Xét hàm số y S(x) - 2{x^2} + 20x(0 x 10)a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số y - 2{x^2} + 20xtrên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị y - 2{x^2} + 20x có giống với đồ thị của hàm số y - 2{x^2} hay không?b) Quan sát dạng đồ thị của hàm số y - 2{x^2} + 20x trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.c) Thực hiện phép biến đổi y - 2{x^2} + 20x ...
Đọc tiếp
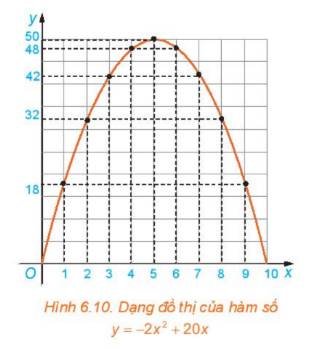
Xét hàm số \(y = S(x) = - 2{x^2} + 20x(0 < x < 10)\)
a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số \(y = - 2{x^2} + 20x\)trên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị \(y = - 2{x^2} + 20x\) có giống với đồ thị của hàm số \(y = - 2{x^2}\) hay không?
b) Quan sát dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\) trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.
c) Thực hiện phép biến đổi \(y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\) Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu.
Vẽ parabol \(y = 3{x^2} - 10x + 7\). Từ đó tìm khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số \(y = 3{x^2} - 10x + 7\).
Gọi (P) là đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\) . Hãy xác định dấu của hệ số a và biệt thức \(\Delta \) , trong mỗi trường hợp sau:
a) (P) nằm hoàn toàn trên trục hoành
b) (P) nằm hoàn toàn dưới trục hoành
c) (P) cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía dưới trục hoành
d) (P) tiếp xúc với trục hoành và nằm phía trên trục hoành
Xác định parabol \(y = {\rm{a}}{{\rm{x}}^2} + bx + 1\) , trong mỗi trường hợp sau:
a) Đi qua 2 điểm A(1; 0) và B(2; 4)
b) Đi qua điểm A(1; 0) và có trục đối xứng \(x = 1\)
c) Có đỉnh I(1; 2)
d) Đi qua điểm C(-1; 1) và có tung độ đỉnh -0,25
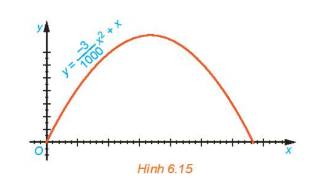
Quỹ đạo của vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình y frac{{ - 3}}{{1000}}{x^2} + x , trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (H.6.15)a) Tím độ cao cực đại của vật trong quá trình bayb) Tính khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
Đọc tiếp
Quỹ đạo của vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) , trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (H.6.15)
a) Tím độ cao cực đại của vật trong quá trình bay
b) Tính khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
Xác định parabol \(y = a{x^2} + bx + c\) , biết rằng parabol đó đi qua điểm A(8; 0) và có đỉnh là I(6; -12)
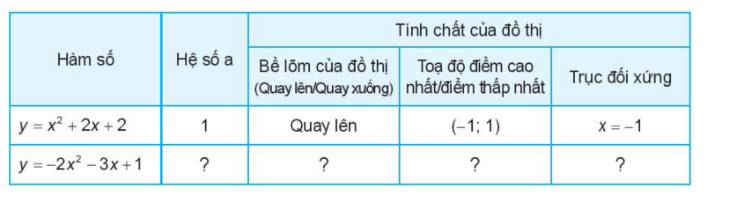
Tương tự HĐ2, ta có dạng đồ thị của một số hàm số bậc hai sau.
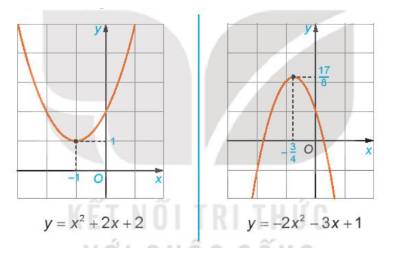
Từ các đồ thị trên, hãy hoàn thành bảng sau đây.