a) Gọi M là trung điểm của BC nên:
Ta có:
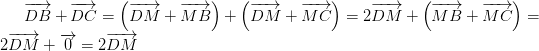
vì 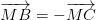
Mặt khác, do D là trung điểm của đoạn AM nên 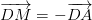
Khi đó: 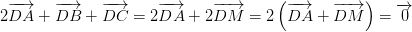
b) Ta có:
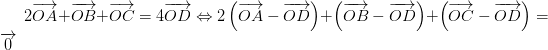
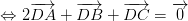 luôn đúng theo câu a
luôn đúng theo câu a
Vậy: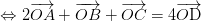 , với O là điểm tùy ý
, với O là điểm tùy ý
a) Gọi M là trung điểm của BC nên:
Ta có:
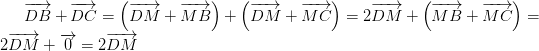
vì 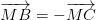
Mặt khác, do D là trung điểm của đoạn AM nên 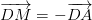
Khi đó: 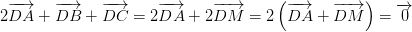
b) Ta có:
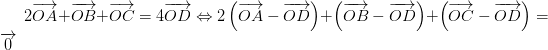
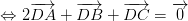 luôn đúng theo câu a
luôn đúng theo câu a
Vậy: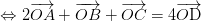 , với O là điểm tùy ý
, với O là điểm tùy ý
Cho tam giác ABC . Gọi A’ la điểm đối xứng của B qua A, B’ là điểm đối xứng với C qua B, C’ là điểm đối xứng của A qua C. với một điểm O bất kỳ.CM :
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'}\)
Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác. D là điểm đối xứng của A qua O
a) Chứng minh tứ giác HCDB là hình bình hành
b) Chứng minh :
\(\overrightarrow{HA}+\overrightarrow{HD}=2\overrightarrow{HO}\)
\(\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=2\overrightarrow{HO}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\)
c) Gọi G là trọng tâm tam giác ABC
Chứng minh \(\overrightarrow{OH}=3\overrightarrow{OG}\). Từ đó kết luận gì về 3 điểm O, H, G ?
Cho tam giác ABC và một điểm M tùy ý . Chứng minh rằng : \(\overrightarrow{4MA}+\overrightarrow{MB}-5\overrightarrow{MC}=4\overrightarrow{CA}+\overrightarrow{CB}\)
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:
\(a.\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=0\)
\(b.\overrightarrow{AM}=\overrightarrow{NB}+\overrightarrow{PC}\)
Cho hình bình hành ABCD , gọi M là trung điểm BC, điểm I thỏa \(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AM}\).Chứng minh rằng \(\overrightarrow{BI}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
cho tam giác ABC có trọng tâm là G và M là trung điểm BC. Khẳng định nào sau đây là sai
A. \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
B. \(\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}\)
C. \(\overrightarrow{GA}=\overrightarrow{BG}+\overrightarrow{GC}\)
D.\(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GM}\)
giúp mk giải câu C , D thôi cx đc tại cô mk bảo phải cm từng câu cho nên m.n giúp mk vs
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đền BC, AC, AB. Chứng minh rằng :
\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\dfrac{3}{2}\overrightarrow{MO}\)
Cho tứ giác ABCD. Gọi E,F,G,H lần lượt là trung điểm của các cạnh AB,BC,CD,DA. M,N là trung điểm BD,AC. O là trung điểm EG. CMR:
a. \(\overrightarrow{AB}\) + \(\overrightarrow{CD}\) = \(\overrightarrow{AD}\) + \(\overrightarrow{CB}\) = 2. \(\overrightarrow{NM}\)
b. \(\overrightarrow{AB}\) + \(\overrightarrow{AC}\) + \(\overrightarrow{AD}\) = 4. \(\overrightarrow{AO}\)
c. \(\overrightarrow{OA}\) + \(\overrightarrow{OB}\) + \(\overrightarrow{OC}\) + \(\overrightarrow{OD}\) = \(\overrightarrow{0}\)
d. \(\overrightarrow{OH}\) + \(\overrightarrow{OF}\) = \(\overrightarrow{OM}\) + \(\overrightarrow{ON}\) = \(\overrightarrow{0}\)
Cho ngũ giác đều ABCDE tâm O. Chứng minh: \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}=\overrightarrow{0}\)