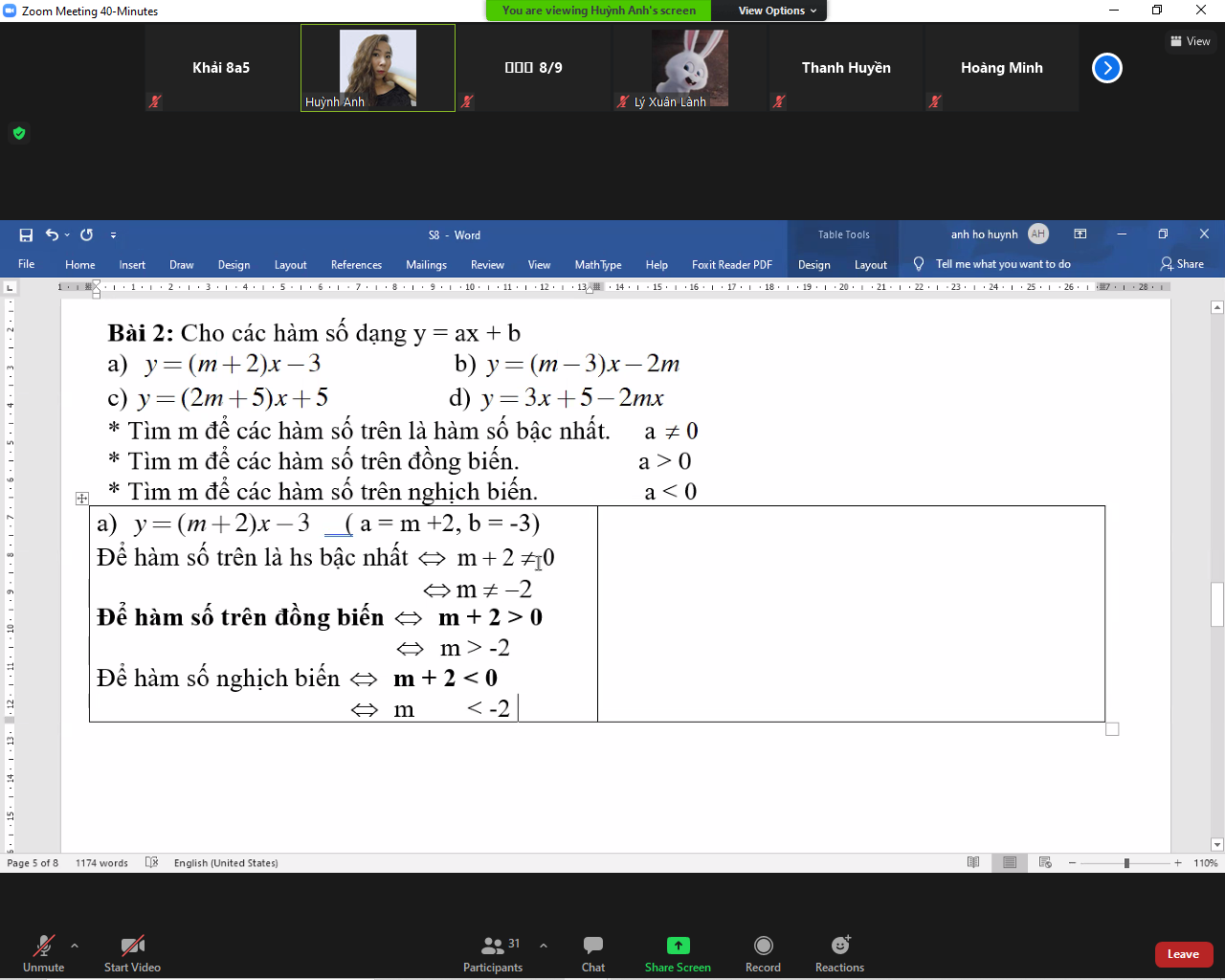
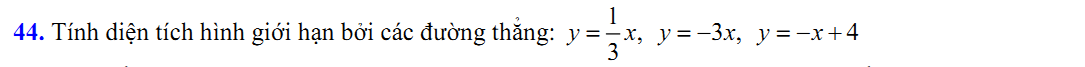a, Cho M(x0;y0) là điểm cố định trên (d)
\(y_0=\left(m+2\right)x_0+m\Leftrightarrow mx_0+2x_0+m-y_0=0\)
\(\Leftrightarrow m\left(x_0+1\right)+2x_0-y_0=0\Rightarrow x_0=-1;y_0=-2\)
Vậy (d) luôn đi qua M(-1;-2)
b, Cho y =0 => \(0=\left(m+2\right)x+m\Leftrightarrow x=-\dfrac{m}{m+2}\)
Vậy (d) cắt trục Ox tại A(-m/m+2;0)
=> OA = |-m/m+2|
Cho x = 0 => \(y=m\)
Vậy (d) cắt trục Oy tại B(0;m) => OB = |m|
Ta có \(S_{AOB}=\dfrac{1}{2}.AO.OB=\dfrac{1}{2}\left|-\dfrac{m}{m+2}.m\right|=\dfrac{1}{2}\left|-\dfrac{m^2}{m+2}\right|=\dfrac{1}{2}\)
\(\Rightarrow\left|\dfrac{m^2}{m+2}\right|=1\Leftrightarrow\left[{}\begin{matrix}m^2=m+2\\m^2=-m-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2;m=-1\\loại\end{matrix}\right.\)
Vậy m = 2 ; m = -1