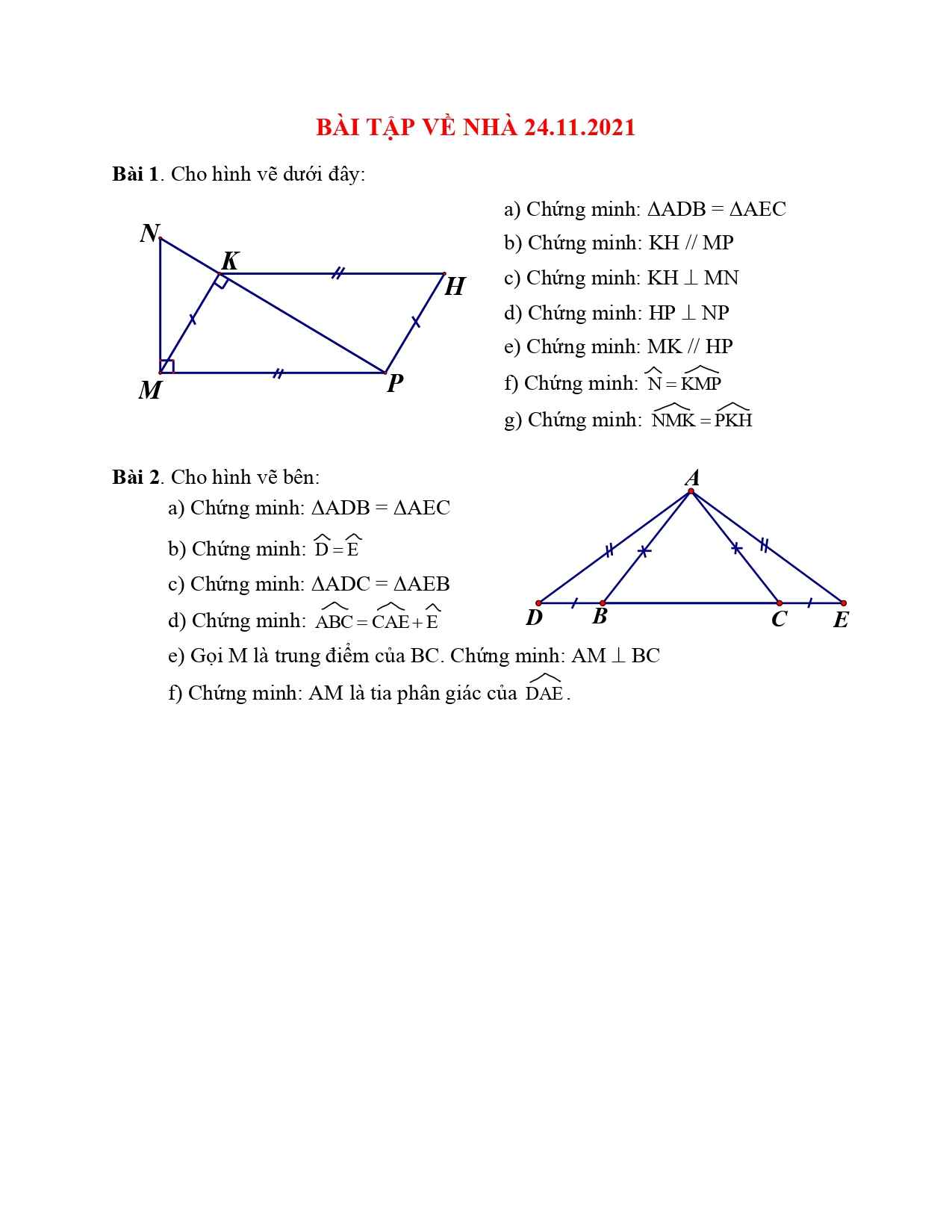
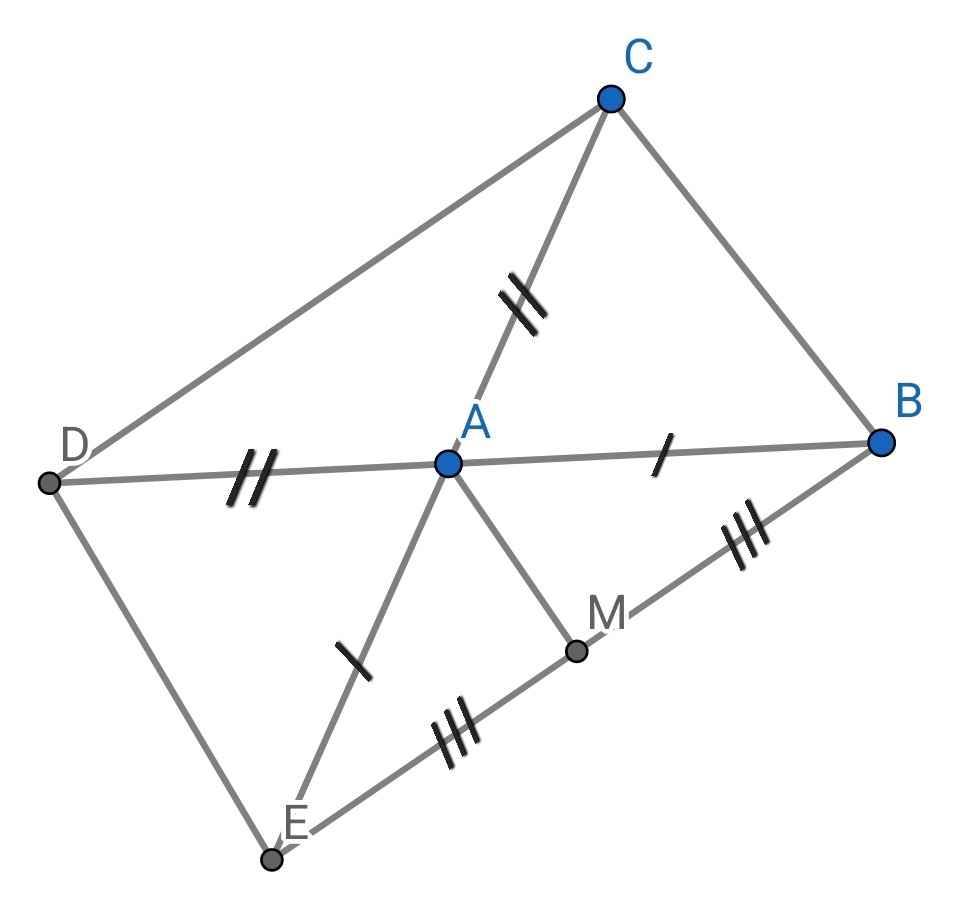
 a) Xét ∆ABC và ∆AED có:
a) Xét ∆ABC và ∆AED có:
AB = AE (gt)
∠BAC = ∠DAE (đối đỉnh)
AC = AD (gt)
⇒ ∆ABC = ∆AED (c-g-c)
⇒ BC = DE (hai cạnh tương ứng)
b) ∆ACD có:
AC = AD (gt)
⇒ ∆ACD cân tại A
∆ABE có:
AB = AE (gt)
⇒ ∆ABE cân tại A
c) Do M là trung điểm của BE (gt)
⇒ MB = ME
Xét ∆ABM và ∆AEM có:
AB = AE (gt)
AM là cạnh chung
MB = ME (cmt)
⇒ ∆ABM = ∆AEM (c-c-c)
⇒ ∠AMB = ∠AME (hai góc tương ứng)
Mà ∠AMB + ∠AME = 180⁰ (kề bù)
⇒ ∠AMB = ∠AME = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BE









 giúp tớ bài này với ạ:3 tớ đang cần gấp
giúp tớ bài này với ạ:3 tớ đang cần gấp


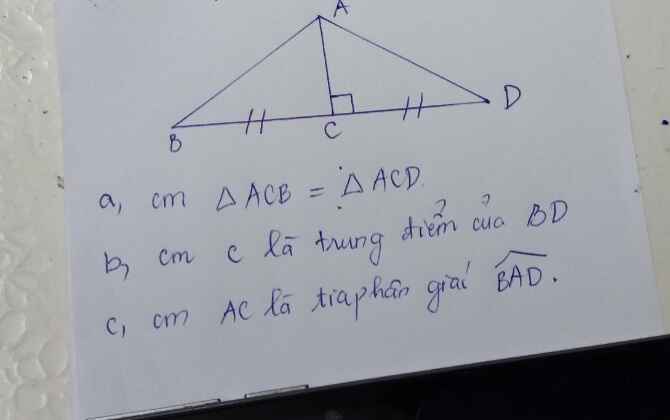 giúp tớ với, tớ đang cần gấp ạ.
giúp tớ với, tớ đang cần gấp ạ.