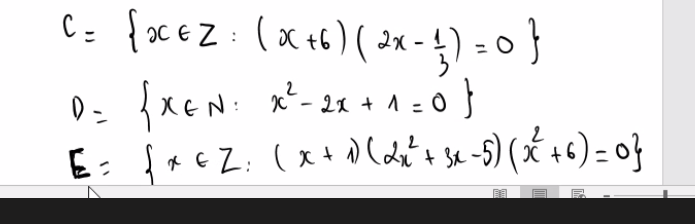\(C_RA=[m;+\infty)\Rightarrow C_RA\cap B=\varnothing\Leftrightarrow2m+2< m\Rightarrow m< -2\)
22/ Với \(n=2k\Rightarrow n^2+1=4k^2+1\) chia 4 dư 1
Với \(n=2k+1\Rightarrow n^2+1=\left(4k^2+4k+2\right)\) chia 4 dư 2
Vậy với mọi n thì \(n^2+1\) đều ko chia hết cho 4, đáp án B sai
23/ Để \(B\subset A\Rightarrow m\ge2\)
26/ Để \(B\subset A\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m+1\le3\end{matrix}\right.\) \(\Rightarrow1\le m\le2\)
27/ Để \(A\cap B=\varnothing\Leftrightarrow\left[{}\begin{matrix}1-2m\le m+3\\m+3< 8-5m\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\le-\frac{2}{3}\\m< \frac{5}{6}\end{matrix}\right.\) \(\Rightarrow-\frac{2}{3}\le m< \frac{5}{6}\)
29/ \(B=\left\{-2;2\right\}\)
Để \(B\backslash A=B\Rightarrow A\cap B=\varnothing\)
\(\Rightarrow\left\{{}\begin{matrix}\left|-2m-3\right|\ne-2m-3\\\left|2m-3\right|\ne2m-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-2m-3< 0\\2m-3< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-\frac{3}{2}\\m< \frac{3}{2}\end{matrix}\right.\)
\(\Rightarrow-\frac{3}{2}< m< \frac{3}{2}\)
Câu 30:
Để hàm số nghịch biến trên R \(\Leftrightarrow2m+3< 0\Rightarrow m< -\frac{3}{2}\)
31/ \(a=1>0\) ; \(-\frac{b}{2a}=2\)
\(\Rightarrow\) Hàm số đồng biến trên \(\left(2;+\infty\right)\) và đồng biến trên \(\left(-\infty;2\right)\)
32/ ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne2\end{matrix}\right.\) hay \([0;+\infty)\backslash\left\{2\right\}\)
33/ Ta có \(x^2-x+1=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\Rightarrow y_{min}=\frac{3}{4}\) khi \(x=\frac{1}{2}\) phù hợp đề bài
Đáp án C
34/ \(f\left(-x\right)=\left|-x+2\right|-\left|-x-2\right|=\left|x-2\right|-\left|x+2\right|=-f\left(x\right)\)
\(f\left(x\right)\) là hàm lẻ
\(g\left(-x\right)=-\left|-x\right|=-\left|x\right|=g\left(x\right)\Rightarrow g\left(x\right)\) là hàm chẵn
35/ \(f\left(2\right)=\frac{2\sqrt{2-2}-3}{2-1}=-3\)
\(f\left(-2\right)=\left(-2\right)^2+2=6\)
\(\Rightarrow f\left(2\right)+f\left(-2\right)=3\)
41/ Hàm chẵn là hàm đối xứng qua Oy
Có 3 hàm (1); (2); (3)
42/ ĐKXĐ: \(\left\{{}\begin{matrix}1+5x\ge0\\7-2x>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge-\frac{1}{5}\\x< \frac{7}{2}\end{matrix}\right.\) \(\Rightarrow-\frac{1}{5}\le x< \frac{7}{2}\)
43/
Trục đối xứng \(x=-\frac{b}{2a}=-1\)
\(f\left(-x\right)=-x^2+2x+1\Rightarrow\) hàm ko chẵn ko lẻ
Do \(a=-1< 0\Rightarrow\) hàm số tăng trên \(\left(-\infty;-1\right)\)
Thay \(x=-1\Rightarrow y=2\Rightarrow I\left(-1;2\right)\) là đỉnh
44/
\(f\left(-x\right)=\left\{{}\begin{matrix}x^3-6;-x\le-2\\\left|x\right|;-2< -x< 2\\-x^3-6;-x\ge2\end{matrix}\right.\)
\(\Rightarrow f\left(-x\right)=\left\{{}\begin{matrix}x^3-6;x\ge2\\\left|x\right|;-2< x< 2\\-x^3-6;x\le-2\end{matrix}\right.\) \(\Rightarrow f\left(-x\right)=f\left(x\right)\)
Hàm đã cho là hàm chẵn
45/ Giống hệt câu 42, chắc do in nhầm
36/ Hàm số đã cho đông biến khi:
\(\left\{{}\begin{matrix}m-1>0\\2-m\ge0\end{matrix}\right.\) \(\Rightarrow1< m\le2\)
37/ \(y=\frac{2\left(x^2+1\right)+x^2+2x+1}{x^2+1}=2+\frac{\left(x+1\right)^2}{x^2+1}\ge2\)
Đáp án đúng là D, ko cần tìm cận trên vì chỉ có D là có cận dưới phù hợp
38/ Trên các khoảng \(\left(-3;-1\right)\) và \(\left(1;3\right)\) đồ thị hàm số có chiều đi lên nên hàm số đồng biến
Đáp án C
39/ \(a=1>0\) ; \(-\frac{b}{2a}=2\Rightarrow\) hàm số đồng biến trên \(\left(2;+\infty\right)\) và nghịch biến trên \(\left(-\infty;2\right)\)
Lưu ý đáp án C là đáp án đúng vì \(\left(3;+\infty\right)\) là tập con của \(\left(2;+\infty\right)\)
40/ ĐKXĐ: Khi \(x< 2\) : \(-3x+8\ge0\Rightarrow\left\{{}\begin{matrix}x< 2\\x\le\frac{8}{3}\end{matrix}\right.\) \(\Rightarrow x< 2\) (1)
Khi \(x\ge2\): \(x+7\ge0\) (luôn đúng) (2)
Kết hợp (1); (2) \(\Rightarrow D=R\) (lấy hợp chứ ko lấy giao)