Bài cuối:
Áp dụng BĐT AM - GM, ta có:
\(\dfrac{1}{a^2+bc}+\dfrac{1}{b^2+ac}+\dfrac{1}{c^2+ab}\)
\(\le\dfrac{1}{2a\sqrt{bc}}+\dfrac{1}{2b\sqrt{ac}}+\dfrac{1}{2c\sqrt{ab}}\)
\(=\dfrac{1}{2}\left(\dfrac{\sqrt{bc}+\sqrt{ac}+\sqrt{ab}}{abc}\right)\)
\(\le\dfrac{a+b+c}{2abc}\left(\text{đ}pcm\right)\)
Dấu "=" xảy ra khi a = b = c
1)a)Công thức phụ:
Ta có: \(\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}-\sqrt{n}\right)=1\)(hằng đẳn thức số 2)
=\(\sqrt{n+1}-\sqrt{n}=\dfrac{1}{\sqrt{n}+\sqrt{n+1}}\)
Áp dụng công thức, biểu thức trên bằng:
\(-\sqrt{1}+\sqrt{2}-\sqrt{2}+\sqrt{3}-...-\sqrt{99}+\sqrt{100}\)
=\(\sqrt{100}-\sqrt{1}\)
=10-1
=9
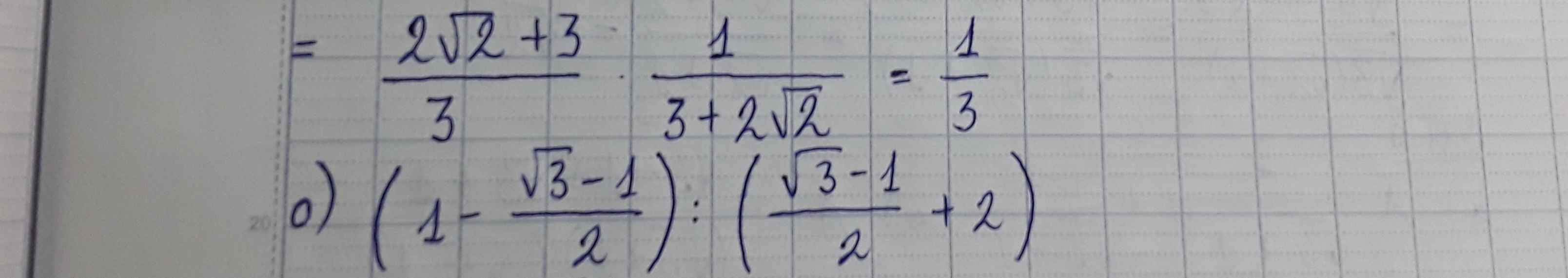giải giúp mk câu o vs ạ
