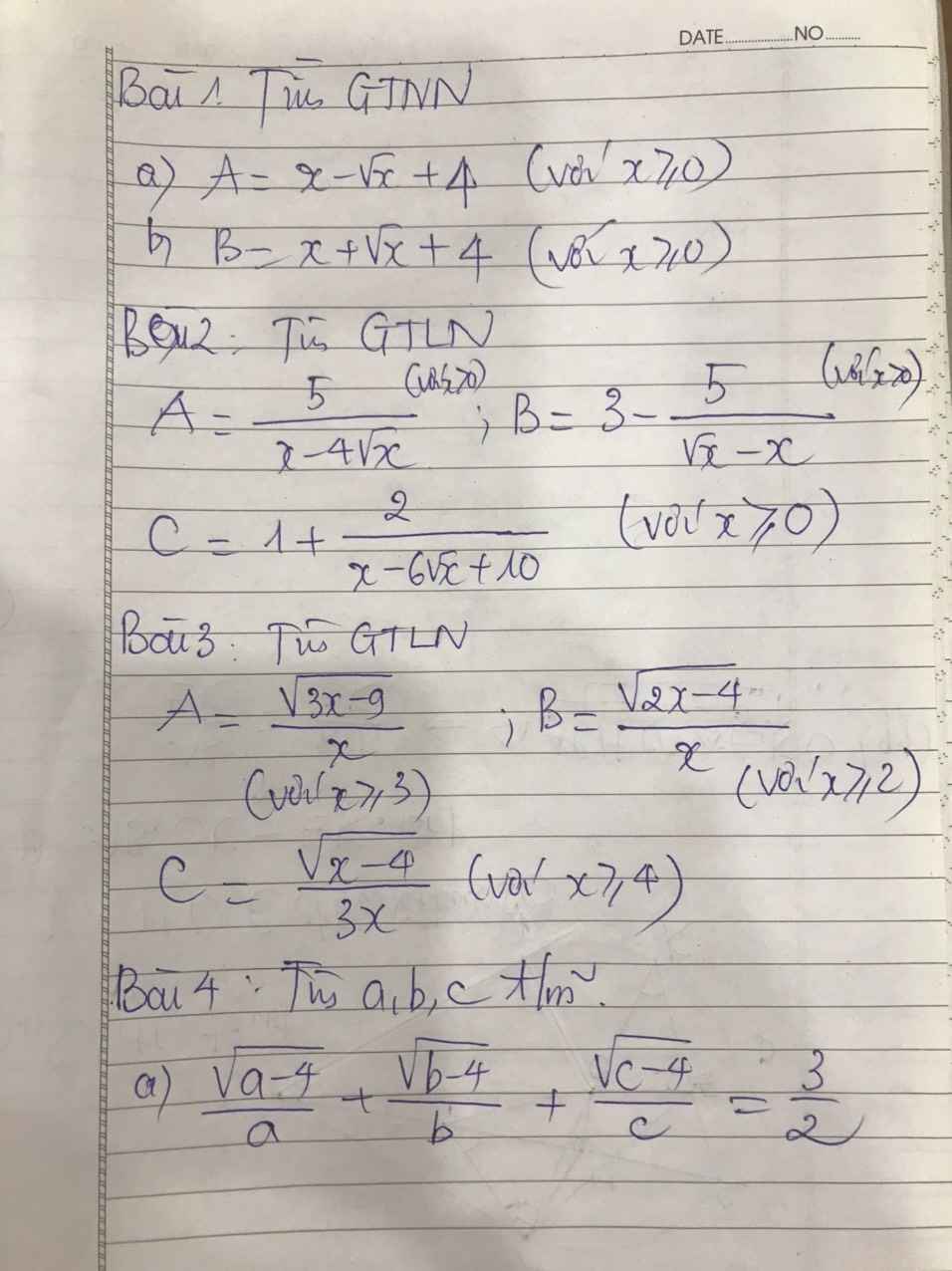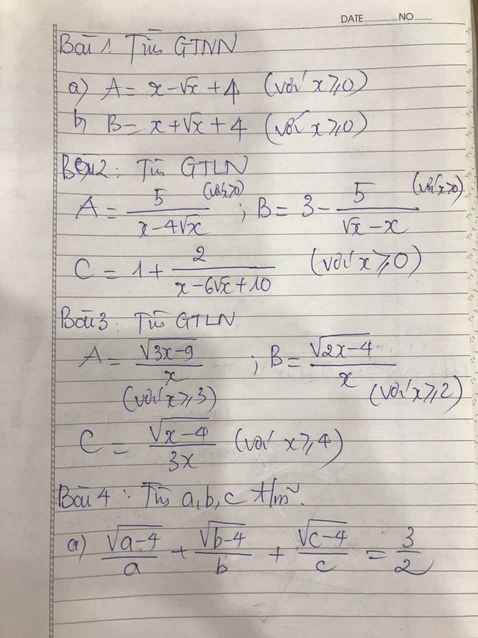\(A=\dfrac{\sqrt{3x-9}}{x}=\sqrt{\dfrac{3x-9}{x^2}}=\sqrt{-\dfrac{9}{x^2}+\dfrac{3}{x}}\)\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{9}{x^2}+2.\dfrac{3}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{3}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{3}{x}-\dfrac{1}{2}=0\Leftrightarrow x=6\) (tm)
Vậy \(A_{max}=\dfrac{1}{2}\)
\(B=\dfrac{\sqrt{2x-4}}{x}=\sqrt{\dfrac{2x-4}{x^2}}=\sqrt{-\dfrac{4}{x^2}+\dfrac{2}{x}}=\sqrt{\dfrac{1}{4}-\left(\dfrac{4}{x^2}-2.\dfrac{2}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{2}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{2}{x}-\dfrac{1}{2}=0\Leftrightarrow x=4\) (tm)
Vậy \(B_{max}=\dfrac{1}{2}\)
\(C=\dfrac{\sqrt{x-4}}{3x}=\sqrt{\dfrac{x-4}{9x^2}}=\sqrt{-\dfrac{4}{9x^2}+\dfrac{1}{9x}}=\sqrt{\dfrac{1}{144}-\left(\dfrac{4}{9x^2}-2.\dfrac{2}{3x}.\dfrac{1}{12}+\dfrac{1}{144}\right)}\)
\(=\sqrt{\dfrac{1}{144}-\left(\dfrac{2}{3x}-\dfrac{1}{12}\right)^2}\le\sqrt{\dfrac{1}{144}}=\dfrac{1}{12}\)
Dấu "=" xảy ra khi \(x=8\) (tm)
Vậy \(C_{max}=\dfrac{1}{12}\)
a) Ta có: \(\dfrac{\sqrt{a-4}}{a}+\dfrac{\sqrt{b-4}}{b}+\dfrac{\sqrt{c-4}}{c}=\dfrac{3}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{a-4}=a\\2\sqrt{b-4}=b\\2\sqrt{c-4}=c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{a-4}=\dfrac{1}{2}a\\\sqrt{b-4}=\dfrac{b}{2}\\\sqrt{c-4}=\dfrac{c}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-4=\dfrac{1}{4}a^2\\b-4=\dfrac{1}{4}b^2\\c-4=\dfrac{1}{4}c^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{4}a^2-a+4=0\\\dfrac{1}{4}b^2-b+4=0\\\dfrac{1}{4}c^2-c+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-4a+16=0\\b^2-4b+16=0\\c^2-4c+16=0\end{matrix}\right.\Leftrightarrow a,b,c\in\varnothing\)