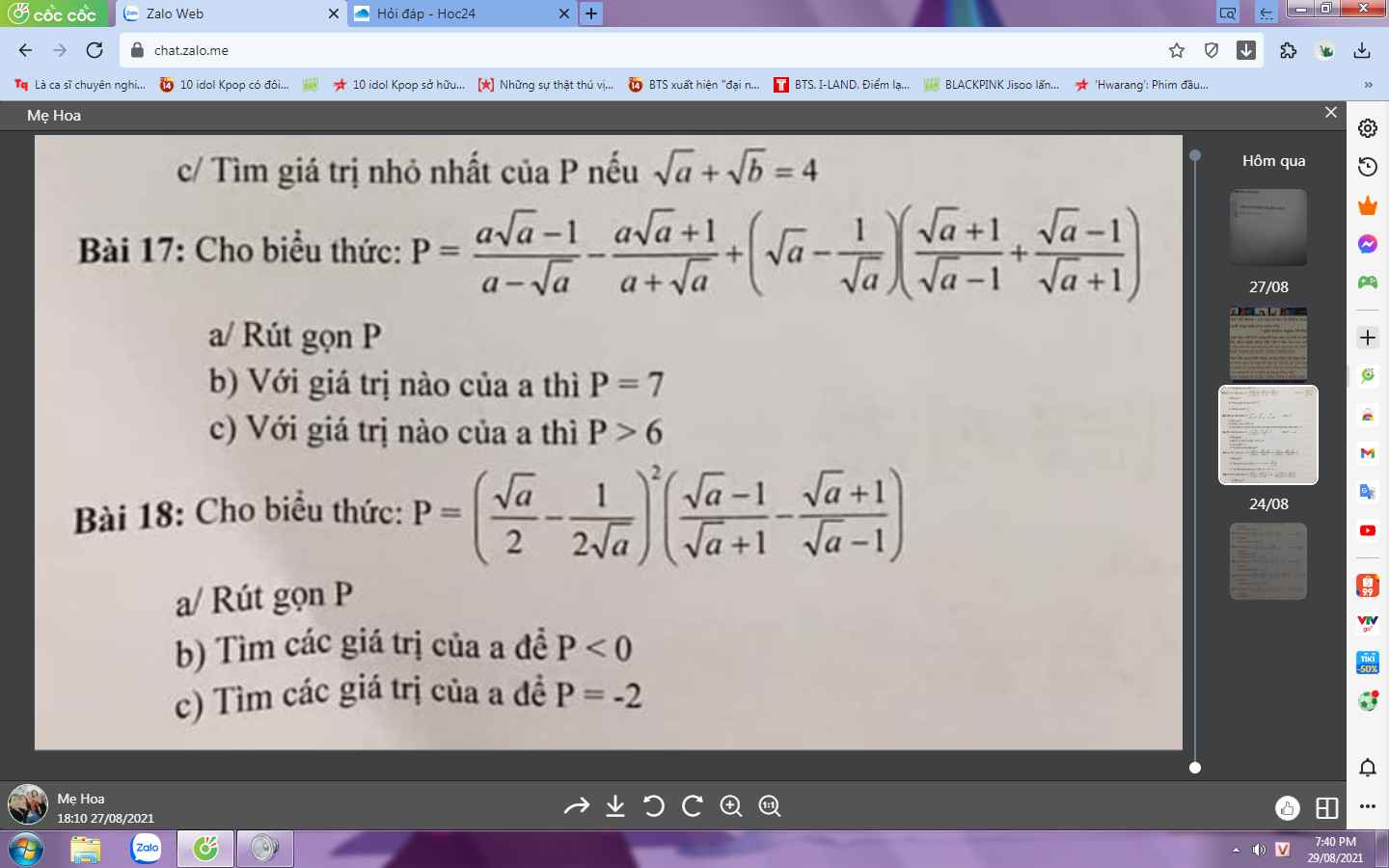
Bài 18:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{\left(a-1\right)\cdot\left(-4\right)\cdot\sqrt{a}}{4a}\)
\(=\dfrac{-a+1}{\sqrt{a}}\)
b: Để P<0 thì -a+1<0
\(\Leftrightarrow-a< -1\)
hay a>1
c: Để P=-2 thì \(-a+1=-2\sqrt{a}\)
\(\Leftrightarrow-a+1+2\sqrt{a}=0\)
\(\Leftrightarrow a-2\sqrt{a}+1=2\)
\(\Leftrightarrow\left(\sqrt{a}-1\right)^2=2\)
\(\Leftrightarrow\sqrt{a}-1=\sqrt{2}\)
hay \(a=3+2\sqrt{2}\)
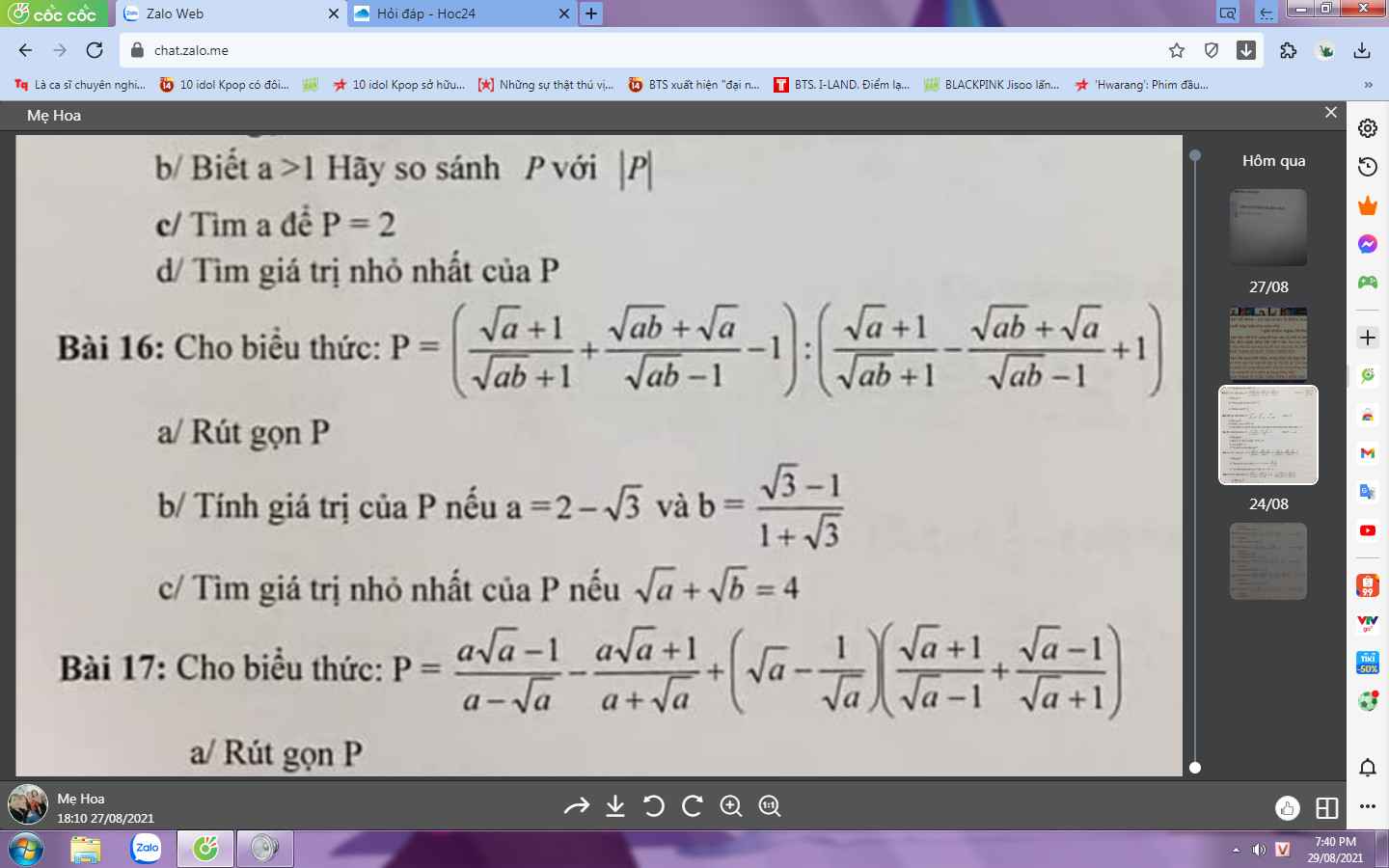
Bài 17:
a: Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\right)\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
\(=2+\dfrac{2a+2}{\sqrt{a}}\)
\(=\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}\)
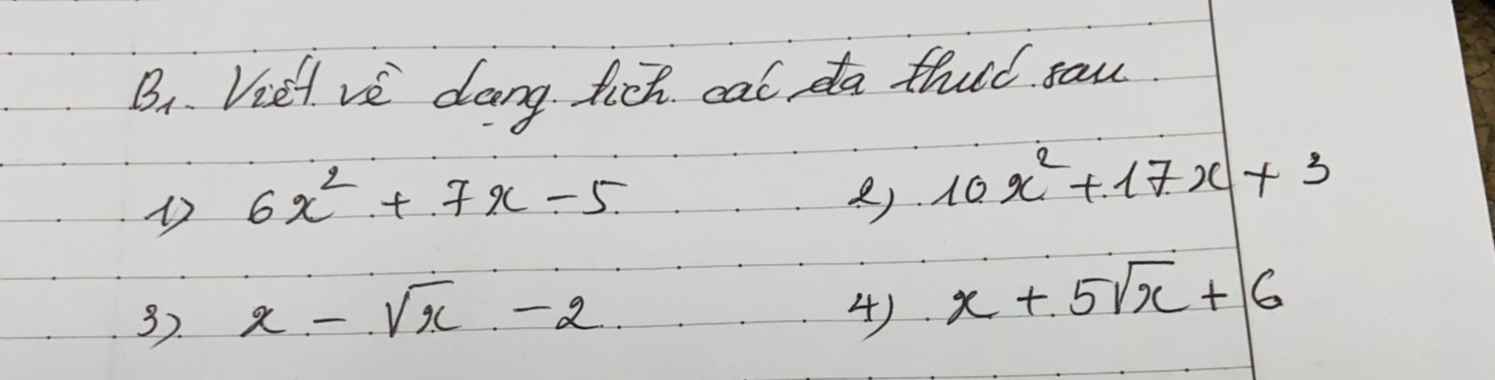
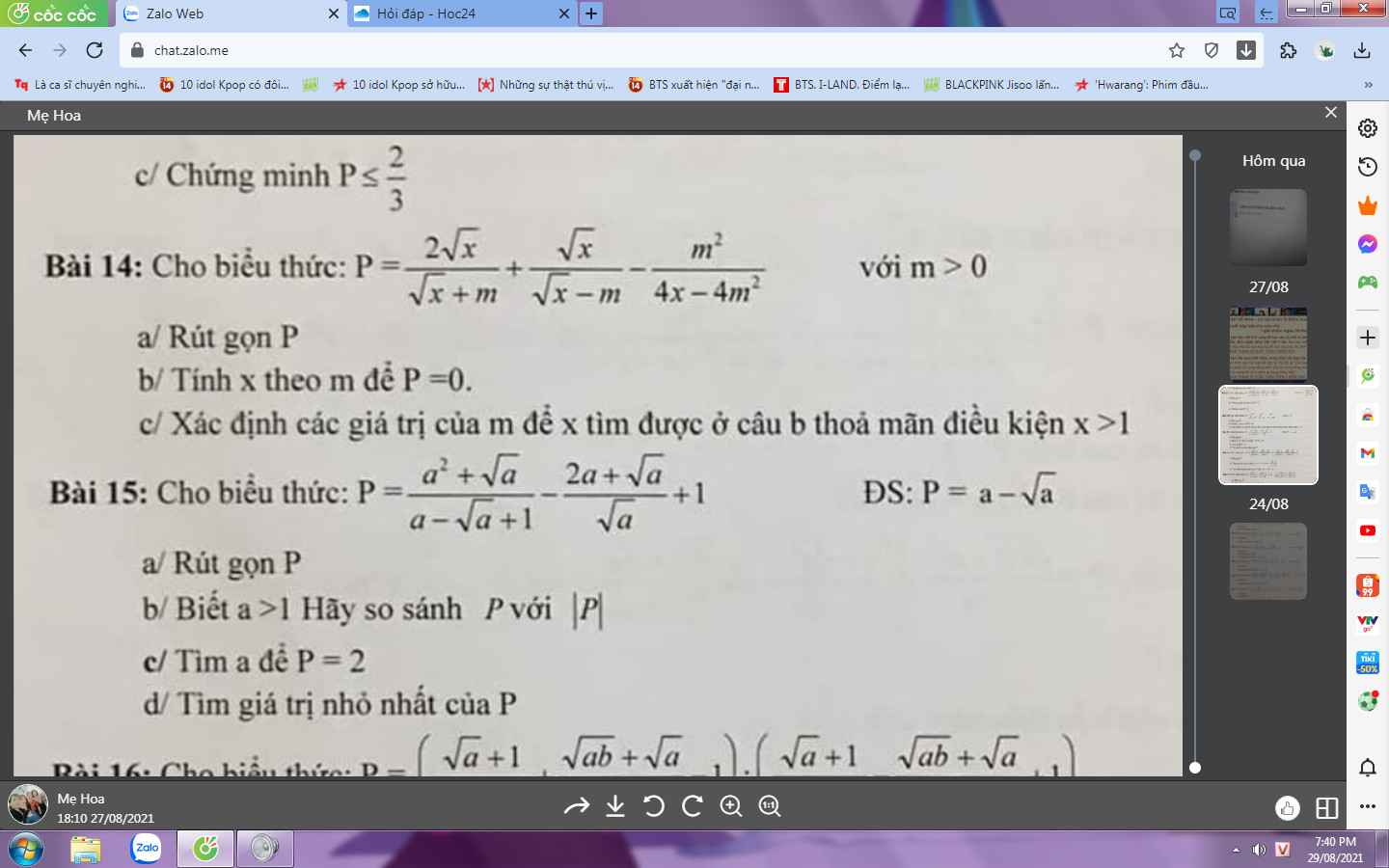
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.