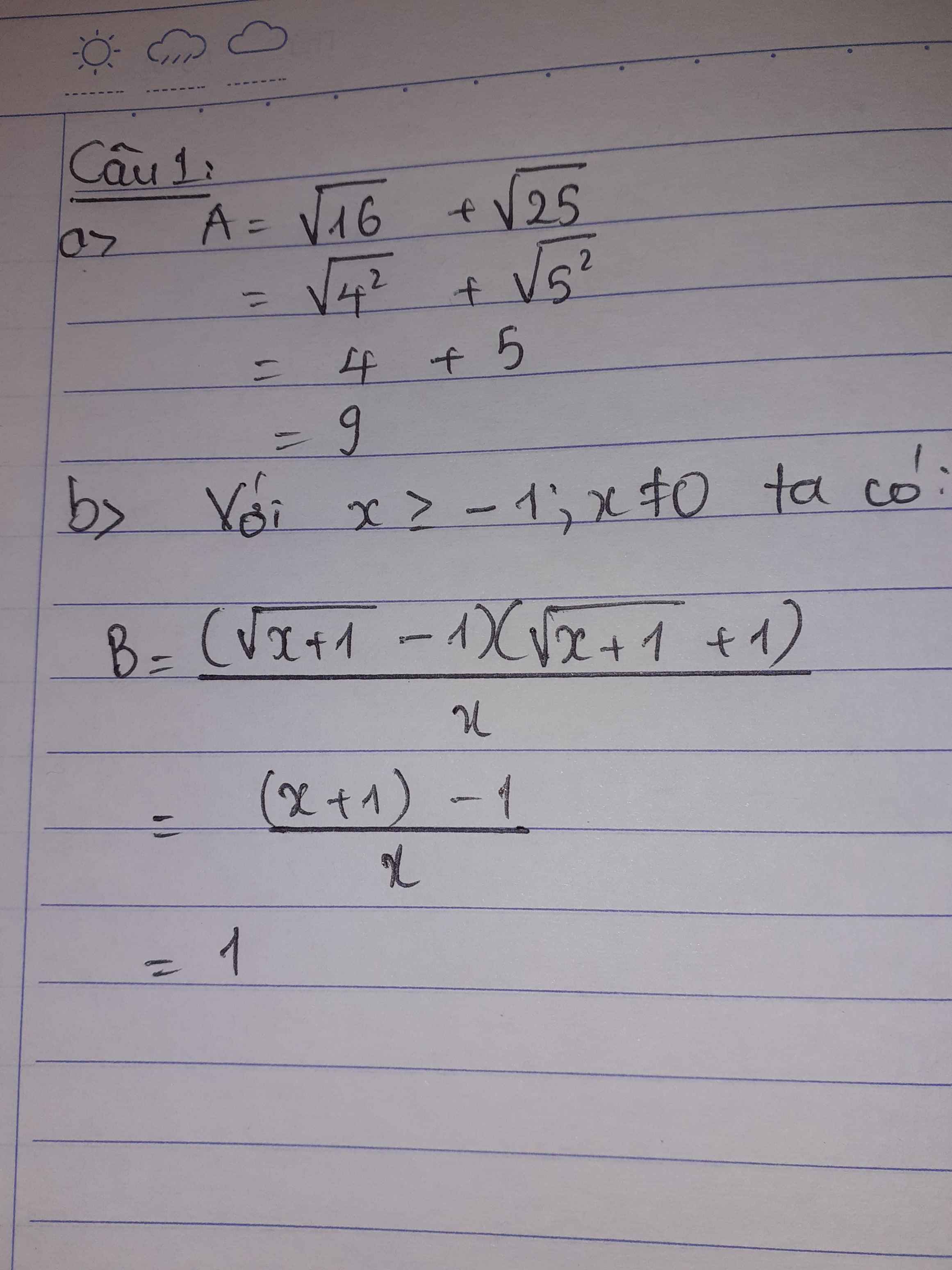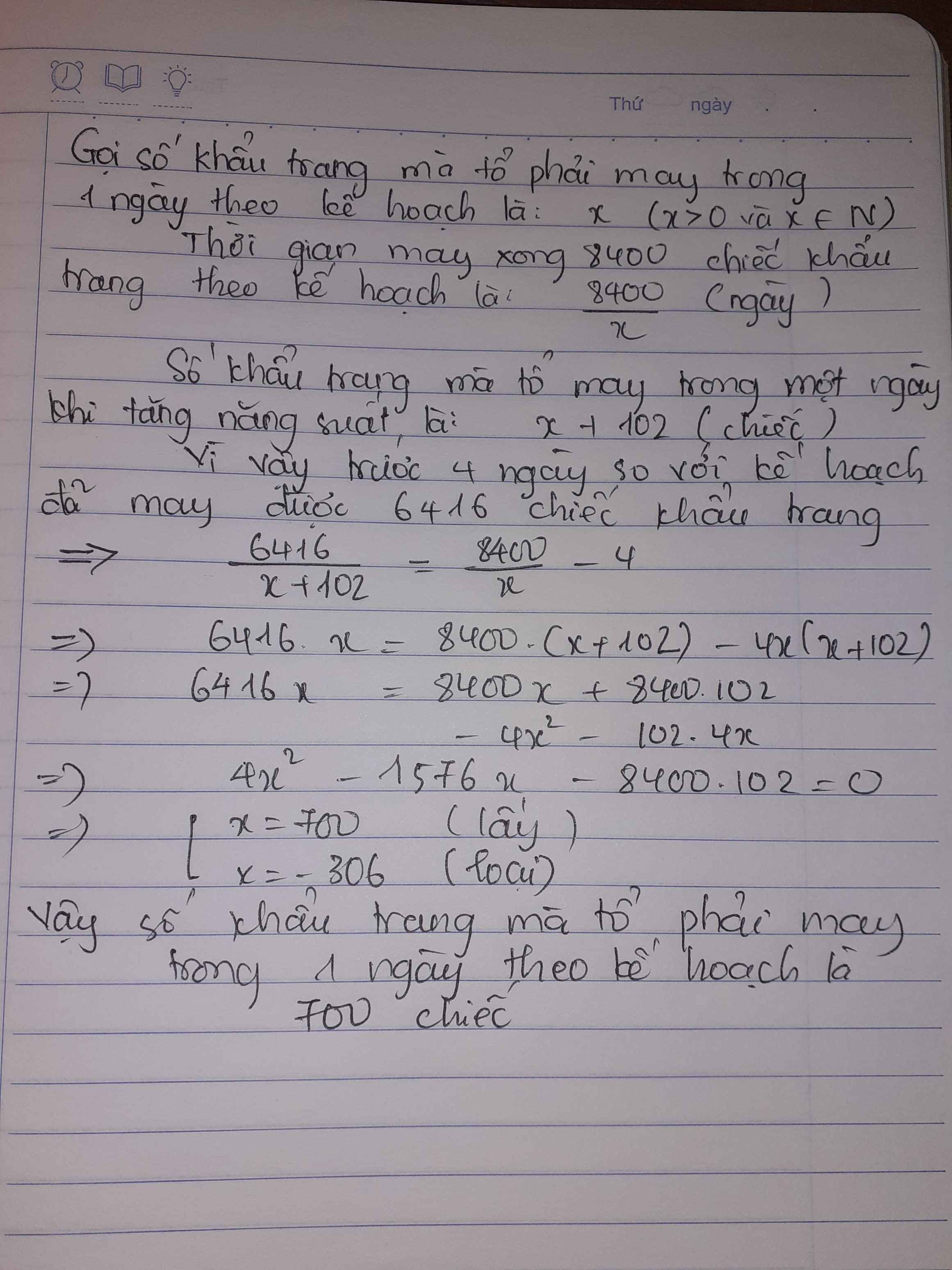1.
\(A=\sqrt{4^2}+\sqrt{5^2}=4+5=9\)
\(B=\dfrac{\left(\sqrt{x+1}-1\right)\left(\sqrt{x+1}+1\right)}{x}=\dfrac{\sqrt{x+1}^2-1^2}{x}=\dfrac{x+1-1}{x}=\dfrac{x}{x}=1\)
5.
Gọi số khẩu trang dự định may mỗi ngày là x>0 (chiếc)
Thời gian dự định may xong: \(\dfrac{8400}{x}\) ngày
Số khẩu trang thực tế mỗi ngày may được: \(x+102\) chiếc
Theo bài ra ta có pt:
\(\left(x+102\right)\left(\dfrac{8400}{x}-4\right)=6416\)
\(\Leftrightarrow x^2-394x-214200=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-306\left(loại\right)\\x=700\end{matrix}\right.\)
Câu 1:
a) Ta có: \(A=\sqrt{16}+\sqrt{25}\)
=4+5
=9
b) Ta có: \(B=\dfrac{\left(\sqrt{x+1}-1\right)\left(\sqrt{x+1}+1\right)}{x}\)
\(=\dfrac{x+1-1}{x}\)
=1
Câu 2:
Ta có: \(\left\{{}\begin{matrix}x-y=3\\3x+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x=4\\y=x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1-3=-2\end{matrix}\right.\)
Vậy: (x,y)=(1;-2)
Câu 6:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4(cm)
Câu 3:
b) Thay x=2 và y=1 vào \(y=ax^2\), ta được:
\(a\cdot2^2=1\)
hay \(a=\dfrac{1}{4}\)
Câu 4:
Ta có: \(x^2-x-3=0\)
a=1; b=-2; c=-3
Vì ac<0 nên phương trình có hai nghiệm phân biệt
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-3\end{matrix}\right.\)
Ta có: \(C=x_1^2+x^2_2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=2^2-2\cdot\left(-3\right)=4+6=10\)