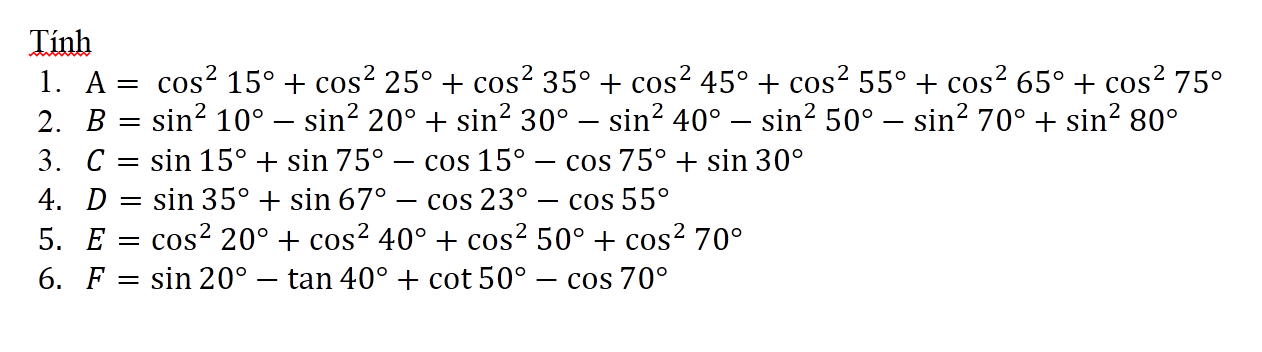1. Ta có: \(cos\alpha=sin\left(90-\alpha\right)\Rightarrow cos75=sin15\Rightarrow cos^275=sin^215\)
Tương tự \(\Rightarrow\left\{{}\begin{matrix}cos^265=sin^225\\cos^255=sin^235\end{matrix}\right.\)
Thế vào đề
\(\Rightarrow A=cos^215+sin^215+cos^225+sin^225+cos^235+sin^235+cos^245\)
\(=1+1+1+\dfrac{\sqrt{2}}{2}=\dfrac{6+\sqrt{2}}{2}\)
câu 2,3,4,5 bạn làm tương tự,dùng\(sin\alpha=cos\left(90-\alpha\right)\) và \(sin^2\alpha+cos^2\alpha=1\) rồi tính thôi
6) Theo như câu a \(\Rightarrow sin20=cos70\)
Lại có: \(tan\alpha=\dfrac{1}{tan\left(90-\alpha\right)}\Rightarrow tan\alpha=cot\left(90-\alpha\right)\Rightarrow cot50=tan40\)
thê vào đề: \(\Rightarrow cos70-cos70+tan40-tan40=0\)