Lời giải:
Do $0< a< \pi$ nên $\cos \frac{a}{2}; \cos \frac{a}{4}>0$
\(2+2\cos a=2(1+\cos a)=2(1+\cos ^2\frac{a}{2}-\sin ^2\frac{a}{2})=2(\cos ^2\frac{a}{2}+\cos ^2\frac{a}{2})=4\cos ^2\frac{a}{2}\)
\(\Rightarrow \sqrt{2+2\cos a}=\sqrt{4\cos ^2\frac{a}{2}}=2\cos \frac{a}{2}\)
\(Q=\sqrt{2+2\cos \frac{a}{2}}=\sqrt{4\cos ^2\frac{a}{4}}=2\cos \frac{a}{4}\)














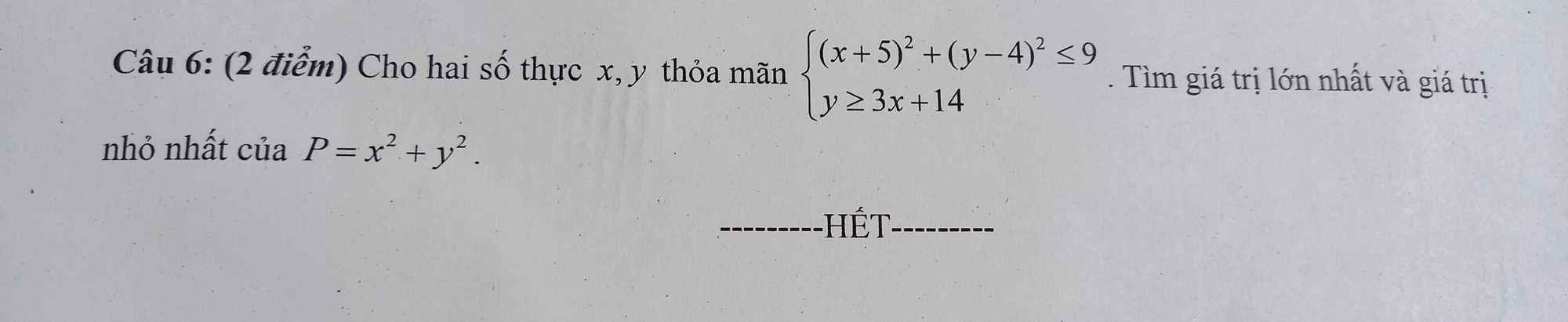
 mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
