6.4
\(y=\dfrac{3}{2}\left(1+cos2x\right)-\sqrt{3}sin2x+\dfrac{1}{2}-\dfrac{1}{2}cos2x\)
\(=cos2x-\sqrt{3}sin2x+2\)
\(=2\left(\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x\right)+2\)
\(=2cos\left(2x-\dfrac{\pi}{3}\right)+2\)
Do \(-1\le cos\left(2x-\dfrac{\pi}{3}\right)\le1\)
\(\Rightarrow0\le y\le4\)
\(y_{min}=0\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\)
\(y_{max}=4\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\)
6.5
Ủa nhìn bài 7 thì đây là chương trình lớp 11 (pt lượng giác) chứ đâu phải lớp 10?
Vậy giải theo kiểu lớp 11 nghe:
\(y=\dfrac{2+cosx+3sinx}{2+cosx}\)
\(\Leftrightarrow2y+y.cosx=2+cosx+3sinx\)
\(\Leftrightarrow3sinx+\left(1-y\right).cosx=2y-2\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(9+\left(1-y\right)^2\ge\left(2y-2\right)^2\)
\(\Leftrightarrow\left(y-1\right)^2\le3\)
\(\Rightarrow1-\sqrt{3}\le y\le1+\sqrt{3}\)
7.
\(\Leftrightarrow\left(m+1\right)\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-3sin^2x.cos^2x\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{4}sin^22x\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{8}\left(1-cos4x\right)\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x=0\)
\(\Leftrightarrow5\left(m+1\right)+\left(3m+11\right)cos4x=0\)
\(\Leftrightarrow\left(3m+11\right)cos4x=-5\left(m+1\right)\)
- Với \(m=-\dfrac{11}{3}\) pt vô nghiệm
- Với \(m\ne-\dfrac{11}{3}\)
\(\Rightarrow cos4x=\dfrac{-5\left(5m+1\right)}{3m+11}\)
Do \(-1\le cos4x\le1\) nên pt có nghiệm khi:
\(-1\le\dfrac{-5\left(m+1\right)}{3m+11}\le1\)
Tới đây chắc bạn tự làm tiếp được đúng ko? Tách ra làm 2 BPT rồi sau đó giao nghiệm thôi
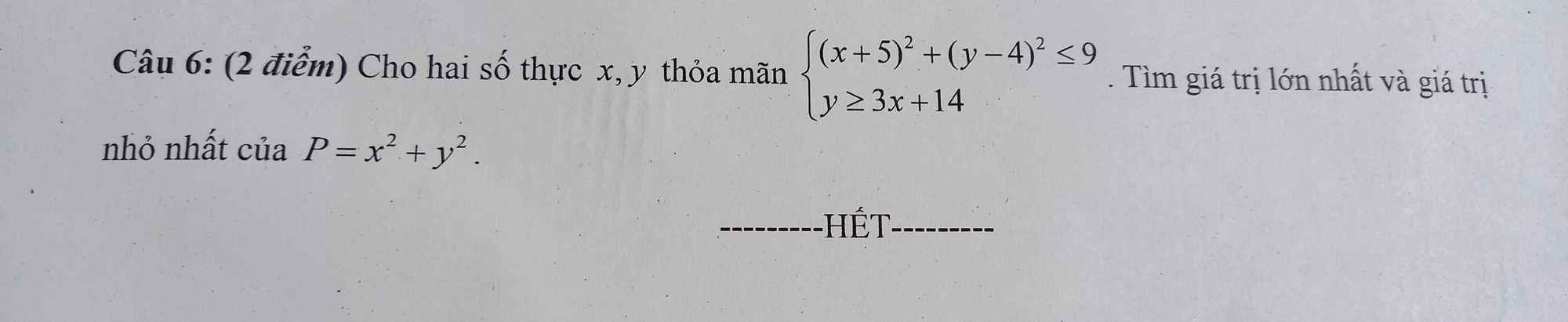
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
