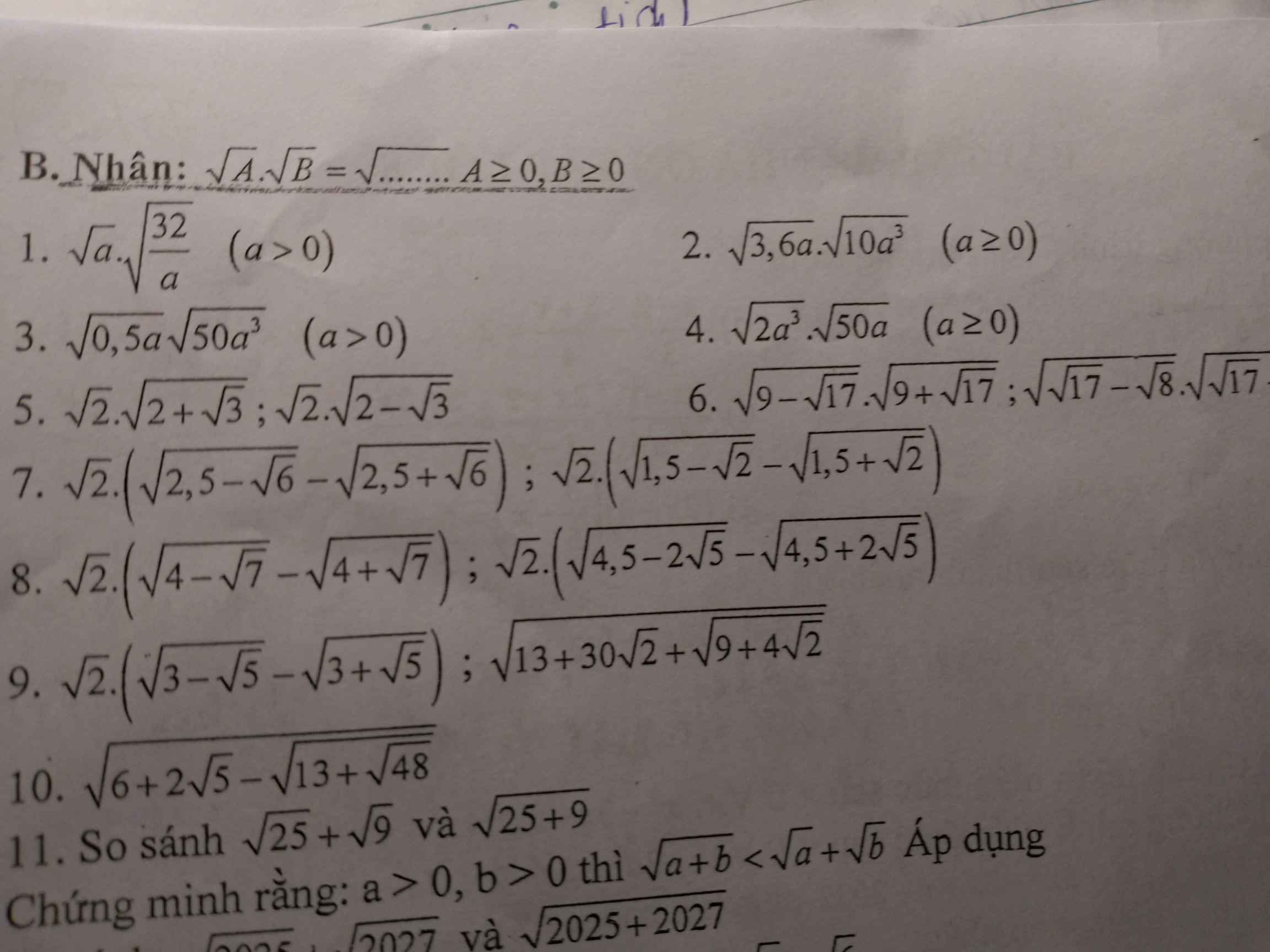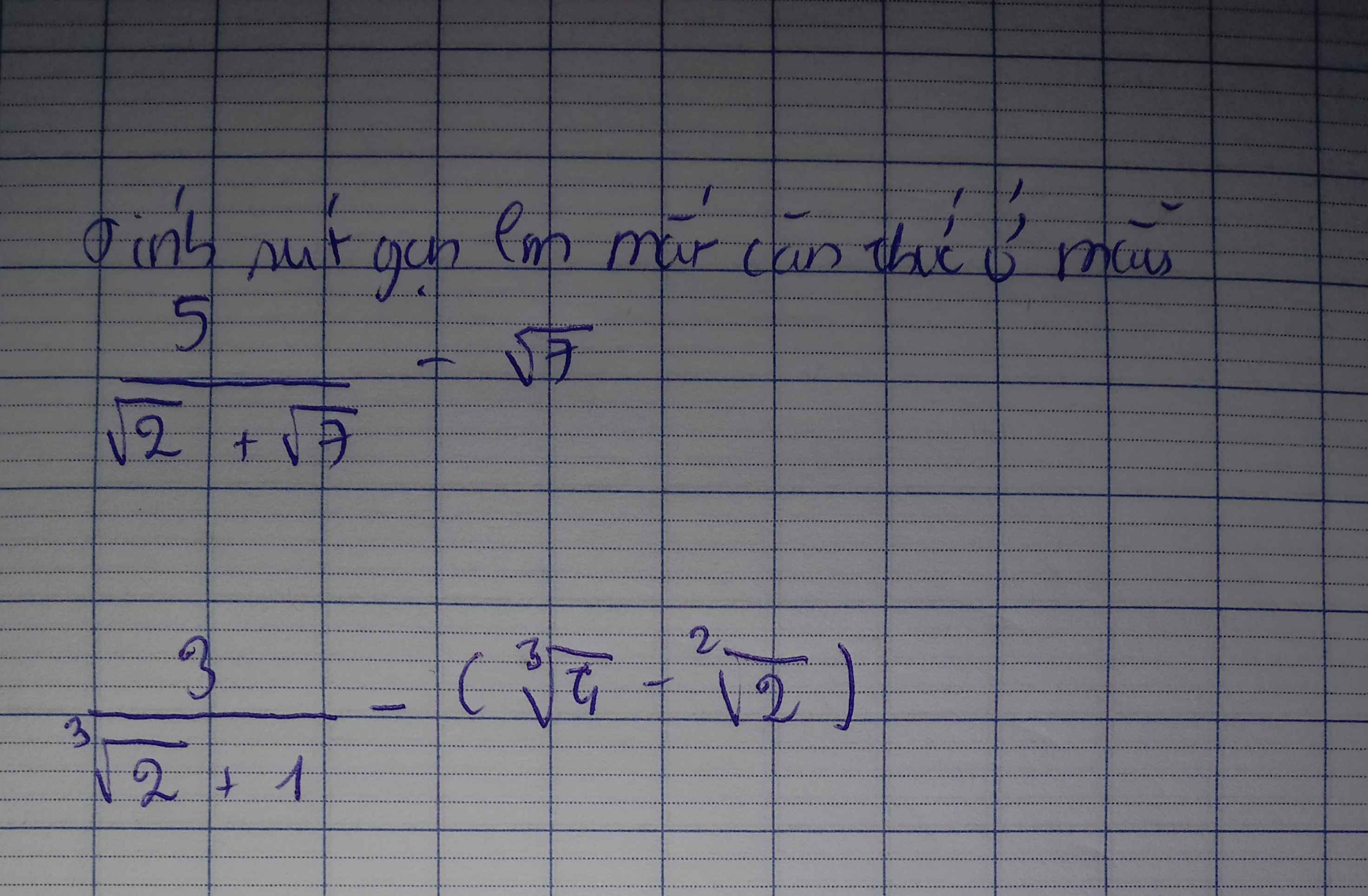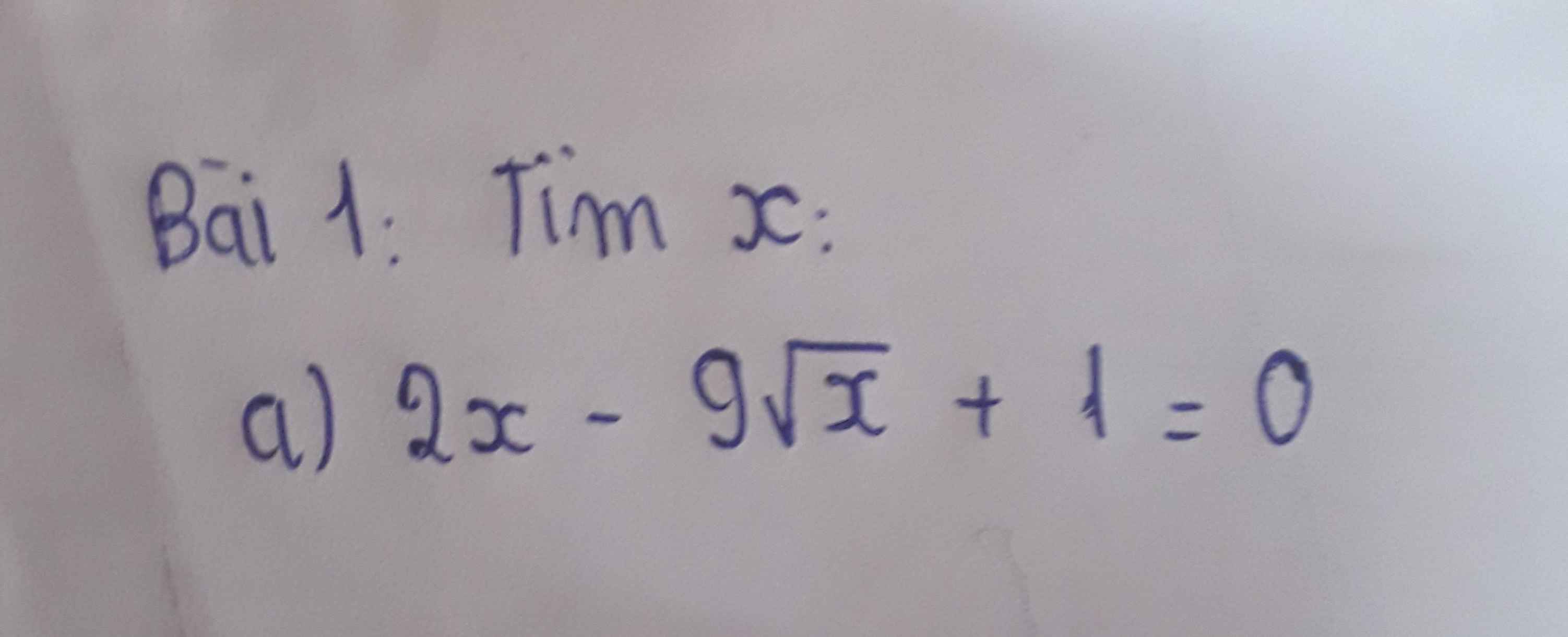a: \(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=32-8\sqrt{15}+8\sqrt{15}-30\)
=2
b: \(=\dfrac{1}{\sqrt{2}}\cdot\left[\left(3-\sqrt{5}\right)\left(\sqrt{5}+1\right)+\left(3+\sqrt{5}\right)\left(\sqrt{5}-1\right)\right]\)
\(=\dfrac{1}{\sqrt{2}}\left(3\sqrt{5}+3-5-\sqrt{5}+3\sqrt{5}-3+5-\sqrt{5}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot4\sqrt{5}=2\sqrt{10}\)
c: \(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}+1-\sqrt{5}+1\right)-\sqrt{2}=\sqrt{2}-\sqrt{2}=0\)
d: \(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}-1-\sqrt{7}-1\right)+\sqrt{7}=-\sqrt{2}+\sqrt{7}\)
e: \(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12}+1+\sqrt{12}-1\right)+2\sqrt{6}=2\sqrt{6}+2\sqrt{6}=4\sqrt{6}\)





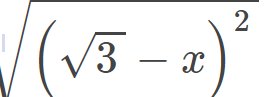
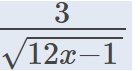 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ