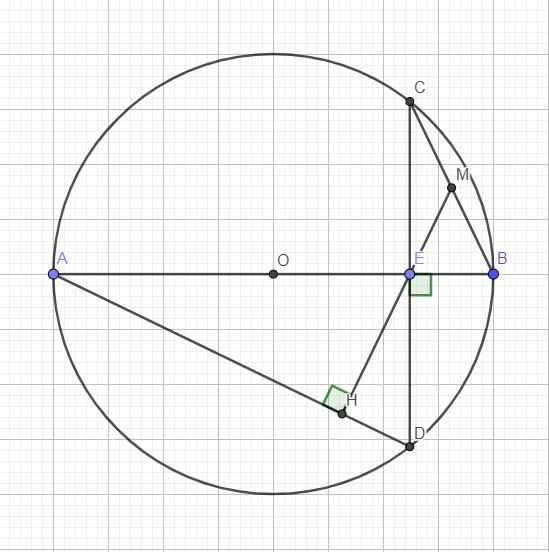
Tứ giác ACBD nội tiếp \(\Rightarrow\widehat{ADC}=\widehat{ABC}\) (cùng chắn AC) (1)
Lại có \(\widehat{ADC}+\widehat{DEH}=90^0\) (tam giác DEH vuông tại H theo gt) (2)
Gọi M là trung điểm BC, nối EM
Trong tam giác vuông BCE, EM là trung tuyến ứng với cạnh huyền
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\Rightarrow\Delta BEM\) cân tại M
\(\Rightarrow\widehat{ABC}=\widehat{MEB}\) (3)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow\widehat{DEH}+\widehat{MEB}=90^0\)
\(\Rightarrow\widehat{DEH}+\widehat{MEB}+\widehat{DEB}=90^0+90^0=180^0\)
\(\Rightarrow M;E;H\) thẳng hàng hay HE đi qua trung điểm M của BC
Đúng 2
Bình luận (0)
