\(\left(\dfrac{1+b\sqrt{b}}{1+\sqrt{b}}-\sqrt{b}\right)\left(\dfrac{1+\sqrt{b}}{1-b}-b\right)^2\)
=\(\left[\dfrac{\left(1+\sqrt{b}\right)\left(1-\sqrt{b}+b\right)}{1+\sqrt{b}}-\sqrt{b}\right]\)\(\left[\dfrac{\left(1+\sqrt{b}\right)}{\left(1-\sqrt{b}\right)\left(1+\sqrt{b}\right)}\right]^2\)
=\(\left(1-2b+b\right)\left(\dfrac{1}{1-\sqrt{b}}\right)^2\)
=\(\left(1-\sqrt{b}\right)^2\left(\dfrac{1^2}{\left(1-\sqrt{b}\right)^2}\right)\)
kết quả còn bước nữa, kết quả cuối cùng
=1








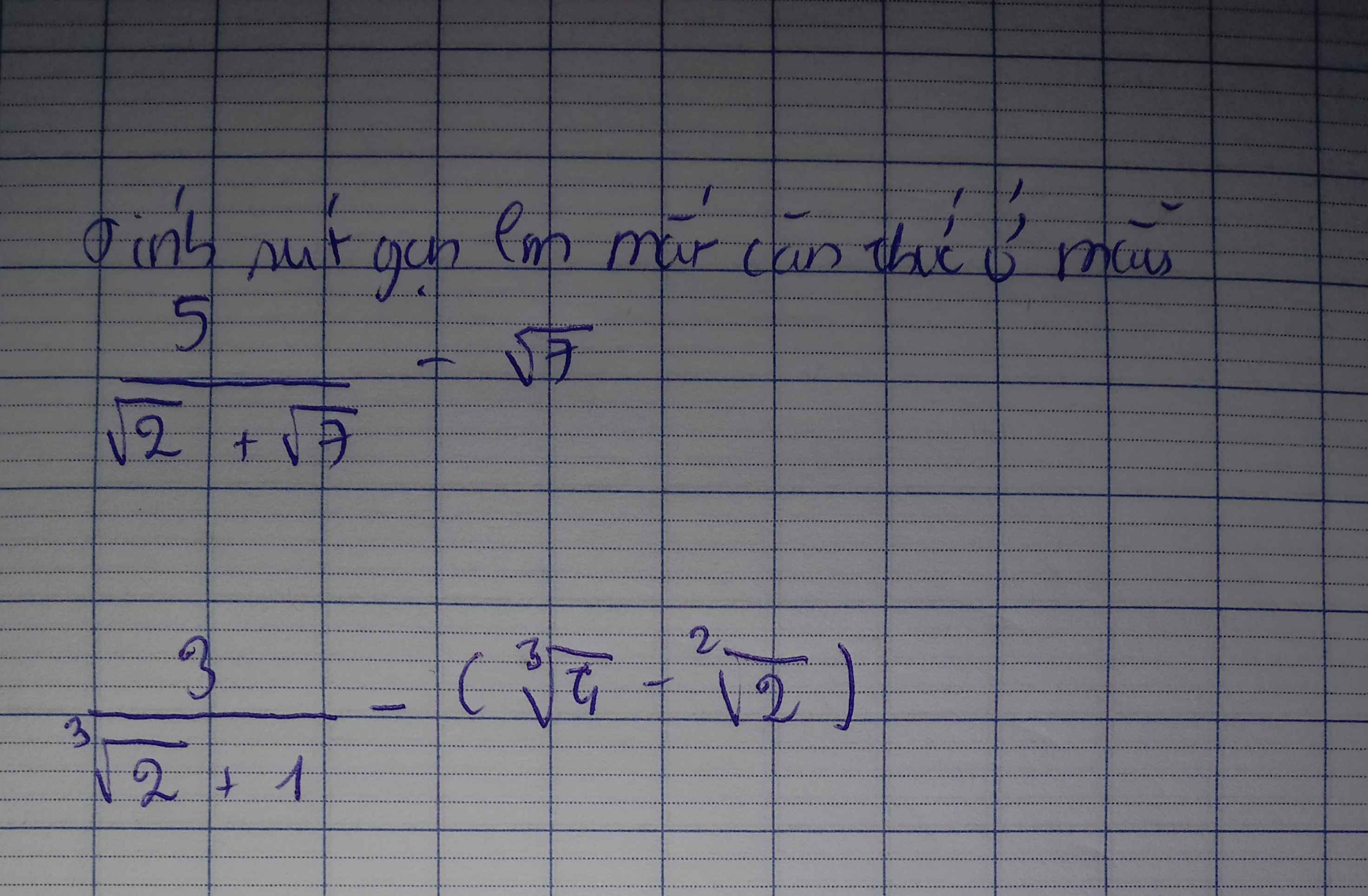

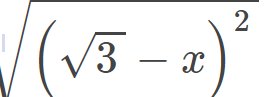
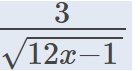 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ