1)
a/ Phép tịnh tiến biến A thành A'
\(\left\{{}\begin{matrix}x'=x+2\\y'=y-4\end{matrix}\right.< =>\left\{{}\begin{matrix}x'=3\\y'=-7\end{matrix}\right.\)
Vậy A'(3:-7) là ảnh của A qua\(\overrightarrow{v}=\left(2;-4\right)\)
b) A thành A'(x'y) qua phép quay tâm O góc 90o
\(\left\{{}\begin{matrix}x=y'\\y=-x'\end{matrix}\right.< =>\left\{{}\begin{matrix}x'=3\\y'=1\end{matrix}\right.\)<=> A'(3;1)
c) A thành A'(x'y) qua phép quay tâm O góc -90o
\(\left\{{}\begin{matrix}x=-y'\\y=x'\end{matrix}\right.< =>\left\{{}\begin{matrix}x'=-3\\y'=-1\end{matrix}\right.\)<=>A'(-3;-1)
d) Phép tịnh tiến biến V(0;-3) biến A thành A'
\(\left\{{}\begin{matrix}x'=0-3.\left(1-0\right)=-3\\y'=0-3.\left(-3-0\right)=9\end{matrix}\right.\)<=>A'(-3;9)
e) Phép tịnh tiến biến V(B;2) biến A thành A' với B(0;-1)
\(\left\{{}\begin{matrix}x'=0+2\left(1-0\right)=2\\y'=-1+2\left(-3-1\right)=-9\end{matrix}\right.\)<=> A'(2;-9)
f) Phép quay tâm O góc 270 biến A thành A'
<=>\(\left\{{}\begin{matrix}x'=1.cos\left(270\right)+3.sin\left(270\right)=3\\y'=-3.cos\left(270\right)+1.sin\left(270\right)=-1\end{matrix}\right.\)<=>A'(3;-1)





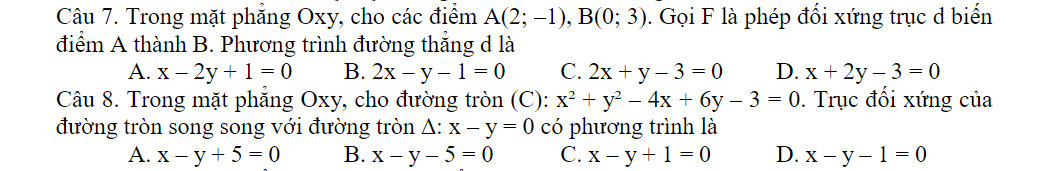 Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều
Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều








