\(\dfrac{1}{1+\sqrt{5}}+\dfrac{1}{1-\sqrt{5}}=\dfrac{1-\sqrt{5}+1+\sqrt{5}}{1-5}=\dfrac{2}{-4}=\dfrac{-1}{2}\)
\(\dfrac{1+\sqrt{5}+1-\sqrt{5}}{\left(1+\sqrt{5}\right)\left(1-\sqrt{5}\right)}=\dfrac{2}{1-5}=-\dfrac{1}{2}\)
\(\dfrac{1}{1+\sqrt{5}}+\dfrac{1}{1-\sqrt{5}}\)
= \(\dfrac{1-\sqrt{5}}{\left(1+\sqrt{5}\right)\left(1-\sqrt{5}\right)}+\dfrac{1+\sqrt{5}}{\left(1+\sqrt{5}\right)\left(1-\sqrt{5}\right)}\)
= \(\dfrac{1-\sqrt{5}}{1^2-\left(\sqrt{5}\right)^2}+\dfrac{1+\sqrt{5}}{1^2-\left(\sqrt{5}\right)^2}\)
= \(\dfrac{1-\sqrt{5}}{1-5}+\dfrac{1+\sqrt{5}}{1-5}\)
= \(\dfrac{1-\sqrt{5}}{-4}+\dfrac{1+\sqrt{5}}{-4}\)
= \(\dfrac{1-\sqrt{5}+1+\sqrt{5}}{-4}\)
= \(\dfrac{2}{-4}\)
= \(\dfrac{-1}{2}\)

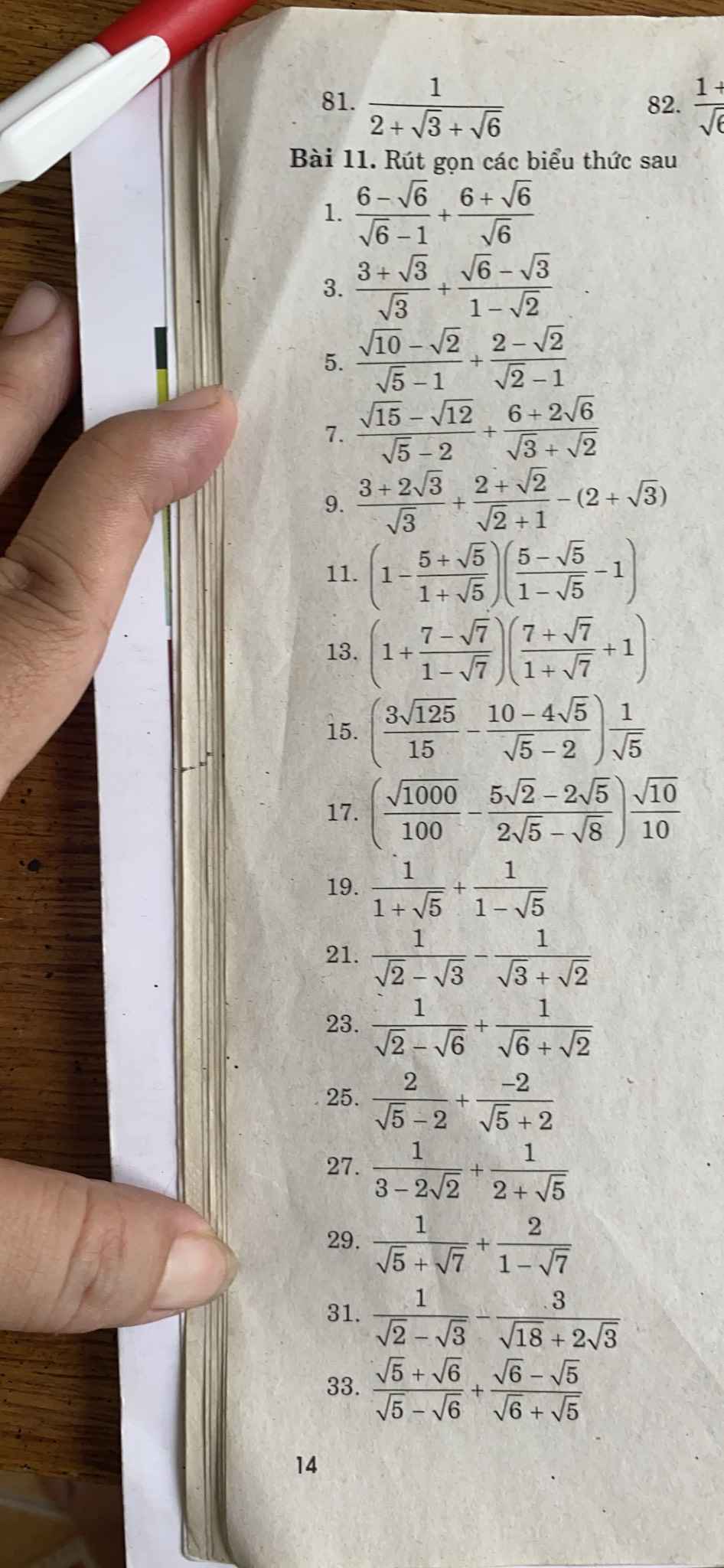









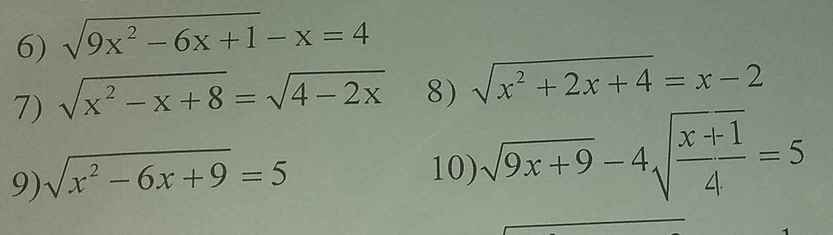











 Giúp mình câu 7,9, mình cảm ơn.
Giúp mình câu 7,9, mình cảm ơn.