\(=\dfrac{5(x+4)}{(x+4)(x-4)}+\dfrac{4(x-4)}{(x+4)(x-4)}-\dfrac{2x-24}{(x+4)(x-4)} \\=\dfrac{7x+28}{(x+4)(x-4)} \\=\dfrac{7(x+4)}{(x+4)(x-4)} \\=\dfrac{7}{x-4}\)
b: \(=\dfrac{5x+20+4x-16-2x+24}{\left(x-4\right)\left(x+4\right)}=\dfrac{7x+28}{\left(x-4\right)\left(x+4\right)}=\dfrac{7}{x-4}\)
\(\dfrac{5}{x-4}+\dfrac{4}{x+4}-\dfrac{2x-24}{x^2-16}=\dfrac{5}{x-4}+\dfrac{4}{x+4}-\dfrac{2x-24}{\left(x-4\right)\left(x+4\right)}=\dfrac{5\text{(x+4)+4(x-4)-2(x-12)}}{\left(x-4\right)\left(x+4\right)}=\dfrac{5x+20+4x-16-\left(2x-24\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{7x+28}{\left(x-4\right)\left(x+4\right)}=\dfrac{7\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{7}{\left(x-4\right)}\)

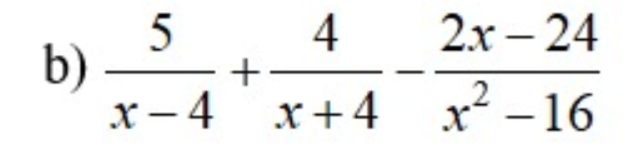















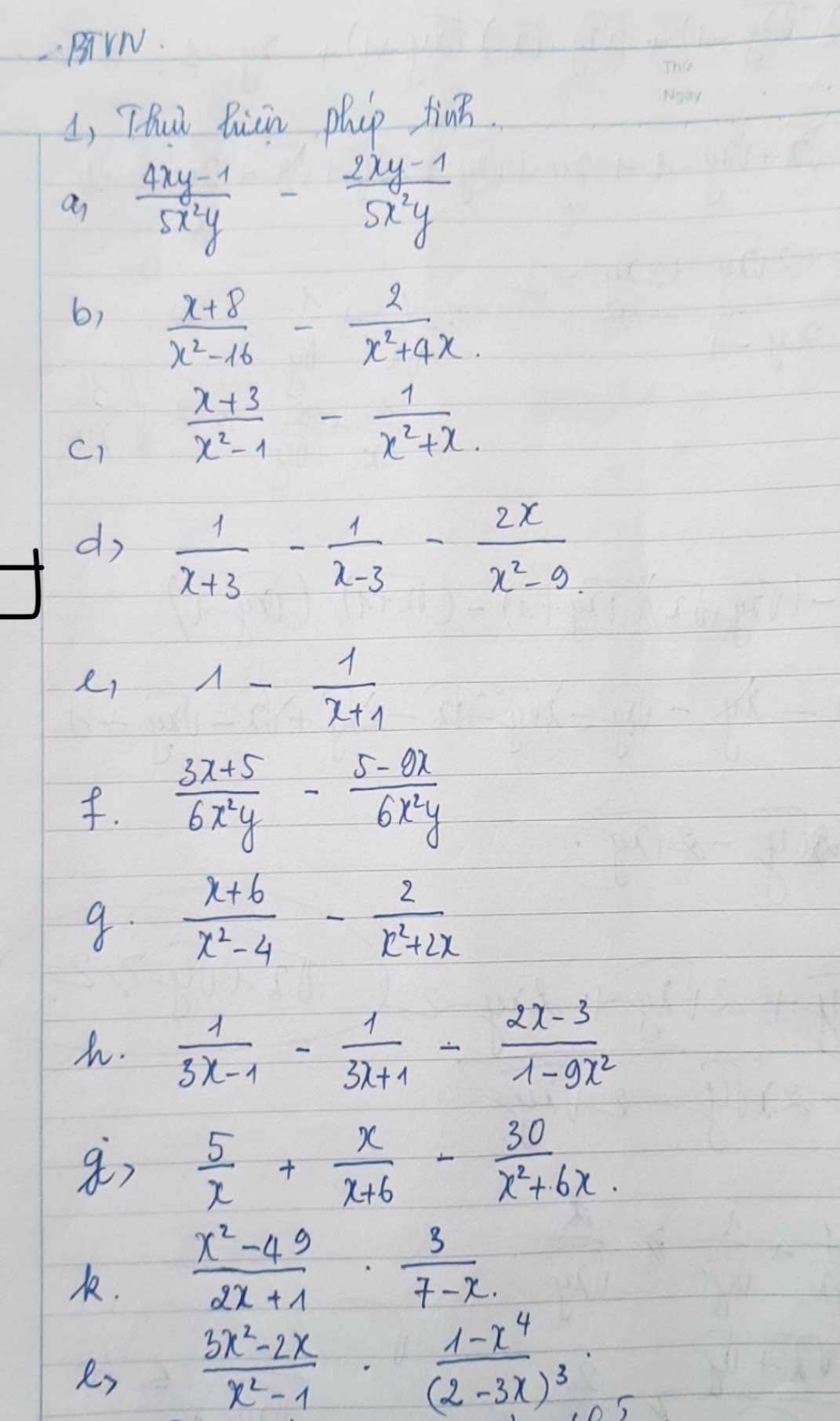


 giúp em với ạ
giúp em với ạ