Gọi độ dài 3 cạnh của tam giác và chiều cao tương ứng của chúng lần lượt là: \(a;b;c;a_1;b_1;c_1\) \(\left(ab,c,a_1,b_1,c_1>0\right)\)
Theo công thức tính diện tích hình tam giác, ta có:
\(a\times a_1\div2=60\Rightarrow a\times a_1=60\times2\Rightarrow a\times a_1=120\Rightarrow a=\dfrac{120}{a_1}\)
\(b\times b_1\div2=60\Rightarrow b\times b_1=60\times2\Rightarrow b\times b_1=120\Rightarrow b=\dfrac{120}{b_1}\)
\(c\times c_1\div2=60\Rightarrow c\times c_1=60\times2\Rightarrow c\times c_1=120\Rightarrow c=\dfrac{120}{c_1}\)
Theo đề bài, ta có: \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) \(\Rightarrow\dfrac{\dfrac{120}{a_1}}{3}=\dfrac{\dfrac{120}{b_1}}{4}=\dfrac{\dfrac{120}{c_1}}{5}\) \(\Rightarrow\dfrac{120}{a_1}\div3=\dfrac{120}{b_1}\div4=\dfrac{120}{c_1}\div5\) \(\Rightarrow\dfrac{120}{3a_1}=\dfrac{120}{4b_1}=\dfrac{120}{5c_1}\) \(\Rightarrow3a_1=4b_1=5c_1\) \(\Rightarrow\dfrac{3a_1}{60}=\dfrac{4b_1}{60}=\dfrac{5c_1}{60}\) \(\Rightarrow\dfrac{a_1}{20}=\dfrac{b_1}{15}=\dfrac{c_1}{12}\)
\(\Rightarrow a_1;b_1;c_1\) tỉ lệ thuận với ba số \(20;15;12\).
Vậy ba chiều cao tương ứng của tam giác tỉ lệ thuận với ba số \(20;15;12\).
Đây nhé bạn :3
https://hoc24.vn/hoi-dap/question/197544.html?pos=678211
Mình nghĩ nên tránh những câu hỏi trùng lặp

 Giúp mình bài này nha mb
Giúp mình bài này nha mb




 Giúp mình nha
Giúp mình nha Giúp tớ nha mn, đang cần gấp lắm. Ai giải hết tick liền luôn nha
Giúp tớ nha mn, đang cần gấp lắm. Ai giải hết tick liền luôn nha Giúp mình cau này nha
Giúp mình cau này nha Ghi cách giải ra giúp mình luôn nha
Ghi cách giải ra giúp mình luôn nha
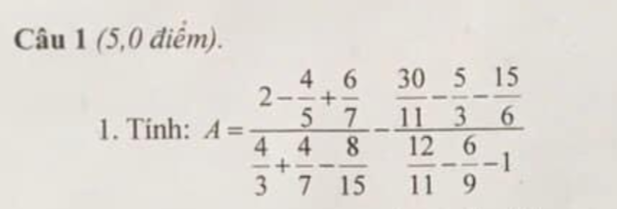
 Ai giúp mình cách trình bày bài này đi ạ, bài 1a,b,c nha
Ai giúp mình cách trình bày bài này đi ạ, bài 1a,b,c nha



 Giúp mình câu này với, vẽ hình giúp mình luôn nha,ngta kêu viết dưới dạng số thập phân
Giúp mình câu này với, vẽ hình giúp mình luôn nha,ngta kêu viết dưới dạng số thập phân