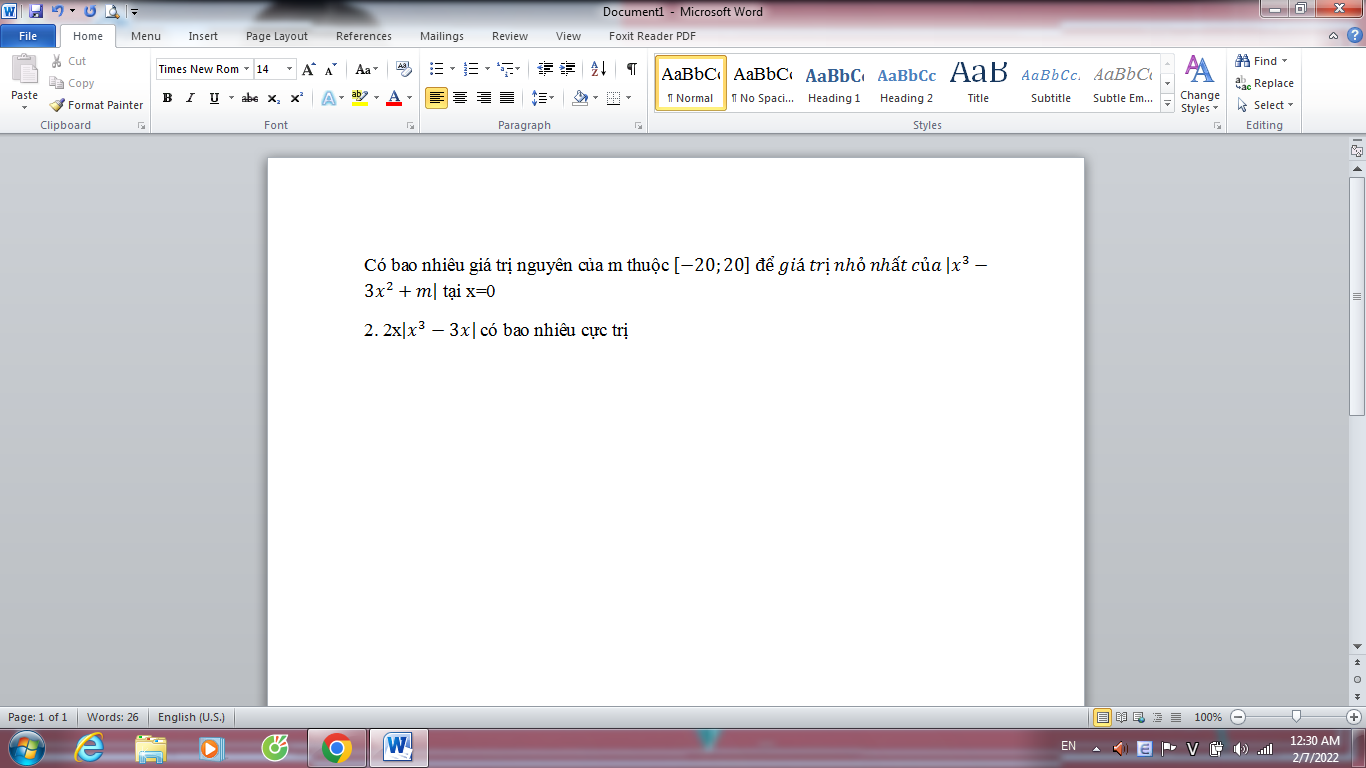
1 Hình như thiếu đề
2. \(f\left(x\right)=\left[{}\begin{matrix}2x\left(x^3-3x\right),x\in\left[-\sqrt{3};0\right]\cup[\sqrt{3};+vc)\\2x\left(3x-x^3\right);x\in\left(-vc,-\sqrt{3}\right)\cup\left(0;\sqrt{3}\right)\end{matrix}\right.\)
\(f'\left(x\right)=\left[{}\begin{matrix}8x^3-12x\\12x-8x^3\end{matrix}\right.\)
Xét \(f'\left(x\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pm\sqrt{6}}{2}\\x=0\end{matrix}\right.\)
Mk làm theo kiểu gộp cả hai biểu thức của f(x) vào chung BBT
4 cực trị
(Cách xét dấu: trong khoảng \(\left[-\sqrt{3};0\right]\cup[\sqrt{3};+vc)\) xét \(f'\left(x\right)=8x^3-12x\) với nghiệm \(x=-\dfrac{\sqrt{6}}{2};x=0\)
trong khoảng \(\left(-vc,-\sqrt{3}\right)\cup\left(0;\sqrt{3}\right)\)xét \(f'\left(x\right)=12x-8x^3\) với nghiệm \(x=\dfrac{\sqrt{6}}{2}\)
Đặt \(f\left(x\right)=x^3-3x^2+m\)
\(f'\left(x\right)=3x^2-6x\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)(tm)
\(x\) \(-2\) \(0\) \(2\)
\(f'\left(x\right)\) || \(+\) \(0\) \(-\) \(0\)
\(f\left(x\right)\) \(-20+m\) \(m\) \(-4+m\)
\(\Rightarrow f\left(x\right)\in\left[-20+m;m\right]\)
\(min\left|f\left(x\right)\right|=min\left\{\left|-20+m\right|,\left|m\right|\right\}\)
Để GTNN của \(\left|f\left(x\right)\right|\) xảy ra tại \(x=0\)
\(\Leftrightarrow\left|m\right|< \left|-20+m\right|\)
\(\Leftrightarrow m< 10\)
Vậy có 30 giá trị của m.