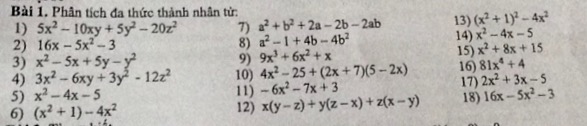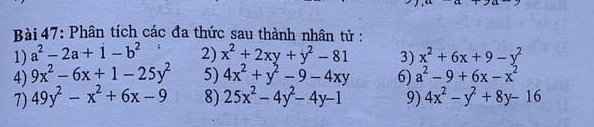1) 5x² - 10xy + 5y² - 20z²
= 5(x² - 2xy + y² - 4z²)
= 5[(x² - 2xy + y²) - 4z²]
= 5[(x - y)² - (2z)²]
= 5(x - y - 2z)(x - y + 2z)
2) 16x - 5x² - 3
= -5x² + 15x + x - 3
= (-5x² + 15x) + (x - 3)
= -5x(x - 3) + (x - 3)
= (x - 3)(-5x + 1)
= (x - 3)(1 - 5x)
3) x² - 5x + 5y - y²
= (x² - y²) - (5x - 5y)
= (x - y)(x + y) - 5(x - y)
= (x - y)(x + y - 5)
4) 3x² - 6xy + 3y² - 12z²
= 3(x² - 2xy + y² - 4z²)
= 3[(x² - 2xy + y²) - 4z²]
= 3[(x - y)² - (2z)²]
= 3(x - y - 2z)(x - y + 2z)
5) x² - 4x - 5
= x² + x - 5x - 5
= (x² + x) - (5x + 5)
= x(x + 1) - 5(x + 1)
= (x + 1)(x - 5)
6) (x² + 1) - 4x²
= 1 - 3x²
= (1 - căn3)(1 + căn3)
2: =-5x^2+15x+x-3
=-5x(x-3)+(x-3)
=(x-3)(-5x+1)
5: =x^2-5x+x-5
=(x-5)(x+1)
6: =-3x^2+1
11: =-6x^2-9x+2x+3
=-3x(2x+3)+(2x+3)
=(2x+3)(-3x+1)
17: =2x^2+5x-2x-5
=(2x+5)(x-1)
15: =x^2+3x+5x+15
=(x+5)(x+3)
14: =x^2-5x+x-5
=(x-5)(x+1)
7) a² + b² + 2a - 2b - 2ab
= (a² - 2ab + b²) + (2a - 2b)
= (a - b)² + 2(a - b)
= (a - b)(a - b + 2)
8) a² - 1 + 4b - 4b²
= a² - (1 - 4b + 4b²)
= a² - (1 - 2b)²
= (a - 1 + 2b)(a + 1 - 2b)
9) 9x³ + 6x² + x
= x(9x² + 6x + 1)
= x(3x + 1)²
10) 4x² - 25 + (2x + 7)(5 - 2x)
= (4x² - 25) - (2x + 7)(2x - 5)
= (2x - 5)(2x + 5) - (2x + 7)(2x - 5)
= (2x - 5)(2x + 5 - 2x - 7)
= -2(2x - 5)
11) -6x² - 7x + 3
= -6x² + 2x - 9x + 3
= (-6x² + 2x) - (9x - 3)
= -2x(3x - 1) - 3(3x - 1)
= (3x - 1)(-2x - 3)
12) x(y - z) + y(z - x) + z(x - y)
= xy - xz + yz - xy + xz - yz
= 0
13) (x² + 1)² - 4x²
= (x² + 1 - 2x)(x² + 1 + 2x)
= (x - 1)²(x + 1)²
14) x² - 4x - 5
= x² + x - 5x - 5
= (x² + x) - (5x + 5)
= x(x + 1) - 5(x + 1)
= (x + 1)(x - 5)
15) x² + 8x + 15
= x² + 3x + 5x + 15
= (x² + 3x) + (5x + 15)
= x(x + 3) + 5(x + 3)
= (x + 3)(x + 5)
16) 81x⁴ + 4
= 81x⁴ + 36x² - 36x² + 4
= (81x⁴ + 36x² + 4) - 36x²
= (9x² + 2)² - (6x)²
= (9x² - 6x + 2)(9x² + 6x + 2)
17) 2x² + 3x - 5
= 2x² - 2x + 5x - 5
= (2x² - 2x) + (5x - 5)
= 2x(x - 1) + 5(x - 1)
= (x - 1)(2x + 5)
18) 16x - 5x² - 3
= -5x² + 15x + x - 3
= (-5x² + 15x) + (x - 3)
= -5x(x - 3) + (x - 3)
= (x - 3)(-5x + 1)