Question

Giúp mik vs mik tik cho ạ.

Answer 1

x+1/3=5/3:2/3

x+1/3=5/2

x=5/2-1/3

x=13/6

Answer 2

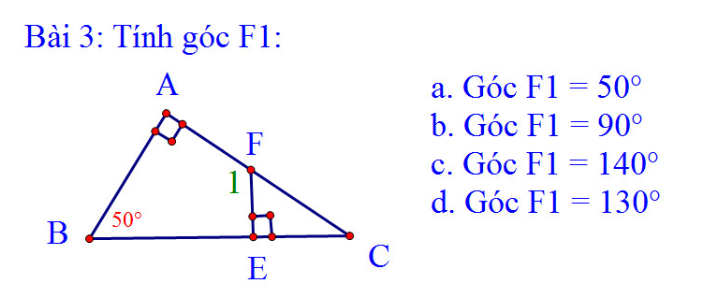
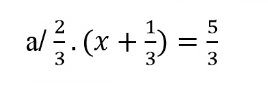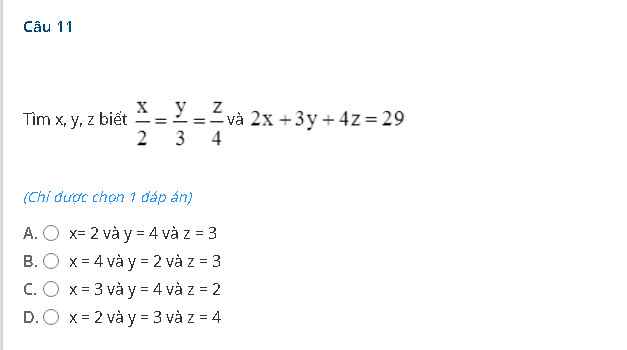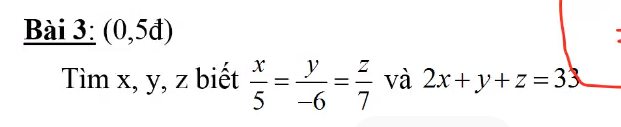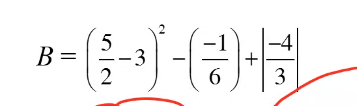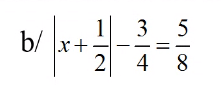\(a,\dfrac{2}{3}.\left(x+\dfrac{1}{3}\right)=\dfrac{5}{3}\)

\(\Rightarrow x+\dfrac{1}{3}=\dfrac{5}{2}\)

\(\Rightarrow x=\dfrac{13}{6}\)

Vậy: \(x=\dfrac{13}{6}\)

Answer 3

\(\Leftrightarrow x+\dfrac{1}{3}=\dfrac{5}{2}\)

hay \(x=\dfrac{5}{2}-\dfrac{1}{3}=\dfrac{13}{6}\)

Answer 4

\(\dfrac{2}{3}x+\dfrac{2}{9}=\dfrac{5}{3}\)

\(\dfrac{2}{3}x=\dfrac{5}{3}-\dfrac{2}{9}\)

\(\dfrac{2}{3}x=\dfrac{15}{9}-\dfrac{2}{9}\)

\(x=\dfrac{13}{9}:\dfrac{2}{3}\)

\(x=\dfrac{13}{6}\)

Vậy...

Answer 5

x + \(\dfrac{1}{3}\) = \(\dfrac{5}{3}\) : \(\dfrac{2}{3}\)
x + \(\dfrac{1}{3}\) = \(\dfrac{5}{3}\) x \(\dfrac{3}{2}\)
x + \(\dfrac{1}{3}\) = \(\dfrac{5}{2}\)
x        =  \(\dfrac{5}{2}\) - \(\dfrac{1}{3}\)
x        =   \(\dfrac{13}{6}\)
Vậy x = \(\dfrac{13}{6}\)