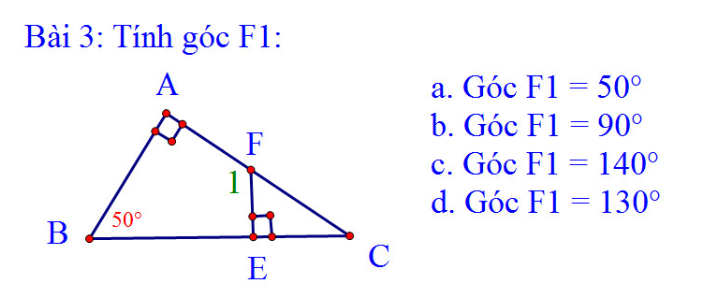
Xét \(\triangle\)\(ABC\) ta có :
\(\widehat{A} + \widehat{B} + \widehat{C} = 180^0\)
Do \(\begin{cases} \widehat{A} = 90^0 \\ \widehat{B} = 50^0\end{cases}\) \(\rightarrow\) \(\widehat{C} = 180^0 - 50^0 - 90^0 = 40^0\)
Xét \(\triangle\)\(CEF\) ta có :
\(\widehat{CEF} + \widehat{C} + \widehat{E} = 180^0\)
Do \(\begin{cases}\widehat{E} = 90^0\\\widehat{C} = 40^0\end{cases}\) \(\rightarrow\) \(\widehat{CEF}\) = \(180^0 - 90^0 - 40^0 = 50^0\)
Ta có : \(\widehat{CEF} + \widehat{F_1} = 180^0\) ( Hai góc kề bù )
Mà \(\widehat{CEF} = 50^0\) \(\rightarrow\widehat{F_1} = 180^0 - 50^0 = 130^0\)
\(\rightarrow D . \widehat{F_1} = 130^0\)