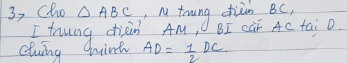Xét △ABC cân tại A:
\(\hat{B}=\dfrac{180°-\hat{A}}{2}=\dfrac{180°-108°}{2}=36°\)
Mà Góc B = Góc C => Góc C = 36°
- BE là tia phân giác góc B, AD là tia phân giác góc A
\(=>\hat{EBC}=\dfrac{36°}{2}=18°\); \(\hat{CAB}=\dfrac{\hat{BAC}}{2}=\dfrac{108°}{2}=54°\)
- Gọi F là trung điểm của CD
- △ABC cân tại A có đường phân giác AD => AD đồng thời là đường trung tuyến, hay: D là trung điểm BC
=> DF là đường trung bình của △CBE
=> DF // BE và \(DF=\dfrac{BE}{2}\)
=> Góc CDF = Góc CBE = 18° (đồng vị)
- Mặt khác: Góc AFD là góc ngoài của △CDF
=> Góc AFD = Góc CDF + Góc FCD
hay: Góc AFD = 18° + 36° = 54°
△ADF có: Góc DAF = Góc AFD = 54°
=> △ADF là tam giác cân => AD = DF
Mà \(DF=\dfrac{BE}{2}\)
Vậy: \(AD=\dfrac{BE}{2}hay:AD=\dfrac{1}{2}BE\left(đpcm\right)\)