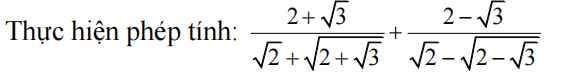Câu II:
a: \(P=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{4\sqrt{x}}{x-1}\right):\left(\dfrac{x+\sqrt{x}+5}{x-1}-\dfrac{1}{\sqrt{x}-1}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x+\sqrt{x}+5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2+4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+5-\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1+4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+4}\)
\(=\dfrac{8\sqrt{x}}{x+4}\)
Câu IV
3: xy-x-y=2
=>xy-x-y+1=3
=>x(y-1)-(y-1)=3
=>(x-1)(y-1)=3
=>\(\left(x-1\right)\cdot\left(y-1\right)=1\cdot3=3\cdot1=\left(-1\right)\cdot\left(-3\right)=\left(-3\right)\cdot\left(-1\right)\)
=>\(\left(x-1;y-1\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(2;4\right);\left(4;2\right);\left(0;-2\right);\left(-2;0\right)\right\}\)
2:
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-4\right)+0\cdot\left(m-3\right)-1\right|}{\sqrt{\left(m-4\right)^2+\left(m-3\right)^2}}\)
\(=\dfrac{1}{\sqrt{2m^2-14m+25}}\)
Để d(O;(d)) lớn nhất thì \(2m^2-14m+25\) nhỏ nhất
\(2m^2-14m+25\)=\(2\left(m^2-7m+12,5\right)\)
\(=2\left(m^2-2\cdot m\cdot\dfrac{7}{2}+\dfrac{49}{4}+\dfrac{1}{4}\right)\)
\(=2\left(m-\dfrac{7}{2}\right)^2+\dfrac{1}{2}>=\dfrac{1}{2}\)
Dấu '=' xảy ra khi m=7/2
Vậy: m=7/2