1: Vì AC vuông góc AB tại A
nên AC là tiếptuyến của (O)
2: góc AFB=1/2*180=90 độ
=>AF vuông góc BG
=>BF*BG=BA^2=BD*BC
=>BF/BD=BC/BG
=>BF/BC=BD/BG
=>ΔBFD đồng dạng với ΔBCG
=>góc BFD=góc BCG
=>góc DFG+góc DCG=180 độ
=>DFGC nội tiếp
Giải giùm em câu d b1. b3 ý 2 câu b và b4 vs ạ
Mn ơi giúp em câu b với ạa, em cám ơn nhiều lắm ạ 
nhanh giùm mọi người ơi em sắp nộp bài rồi câu b,c thôi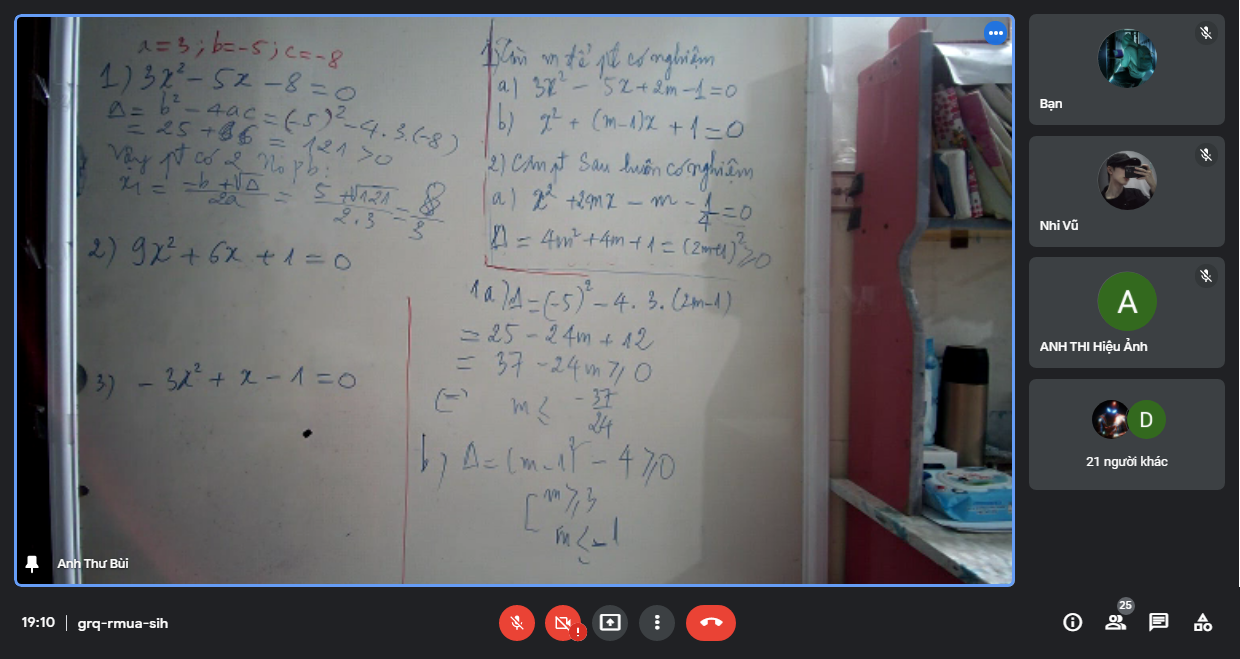
ai giải giùm e chi tiết câu c vs ạ
Gửi giùm mình câu b thôi ạ cảm mơn
ai giả giùm e chi tiết câu b vs ạ
giải giùm e câu c vs ạ
c4
cho pt ẩn x: x2−2x−m2−4=0x2−2x−m2−4=0(1)
a/ giải pt đã cho khi m=1212
b/ chứng minh pt luôn có 2 nghiệm phân biệt vs mọi m
c/ tính giá trị của m để pt (1) có 2 nghiệm x1,x2 sao cho 2x1,x2(2-3x1)=2
Mọi người giúp em giải câu c, d bài hình với. Em chỉ mới giải được a, b (xem bên dưới)
a) Dễ chứng minh \(\Delta ABH\sim \Delta EDH(g.g) \to\angle EDH=\angle ABH.\)
Có \(\angle DEA=\angle EDH=\angle ABH\) nên tứ giác DBCE nội tiếp.
Xét phương trình của điểm A đối với (DBCE) ta có $AD\cdot AB=AE\cdot AC.$
*Chứng minh $DE\bot AO.$
Gọi \(AO\cap DE=\left\{X\right\}\). Ta có:
\(\angle XEA+\angle XAE=\angle ABC+\angle ACB=90^o\Rightarrow \angle AXE=90^o \Rightarrow AO\bot DE.\)
b) Ta có:
\(\angle DAM+\angle DMN=90^o;\angle DMN+\angle HNM=90^o\to\angle DAM=\angle HNM.\)
Tương tự $\angle EAN=\angle HMN.$
Từ đây \(\angle DAM+\angle EAN=90^o\Rightarrow \angle MAN=90^o+\angle BAC=180^o.\)
Vậy \(\overline{M,A,N}\)
Hình vẽ:
Cứu em với giải với giải thích ra hộ em với nhoa câu 5 câu 6 ạ
Giup em với ạaa
