a, Xét ΔAEC và ΔADB có :
\(\widehat{BAC}:chung\)
\(\widehat{AEC}=\widehat{ADB}=90^0\)
\(\Rightarrow\Delta AEC\sim\Delta ADB\left(g-g\right)\)
b, Xét ΔABC có : BD là đường cao thứ nhất (gt)
CE là đường cao thứ hai (gt)
⇒ H là trực tâm ΔABC
⇒ \(AH\perp BC\)
Xét ΔKCH và ΔECB có :
\(\widehat{HKC}=\widehat{BEC}=90^0\)
\(\widehat{BCE}:chung\)
\(\Rightarrow\Delta KCH\sim\Delta ECB\left(g-g\right)\) \(\Rightarrow\dfrac{CH}{BC}=\dfrac{CK}{CE}\Rightarrow CH.CE=BC.CK\left(1\right)\)
c, Dễ thấy \(\Delta KBH\sim\Delta DBC\left(g-g\right)\)
( vì \(\widehat{HKB}=\widehat{BDC}=90^0\) ; \(\widehat{DBC}:chung\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{BH}{BC}\Rightarrow BH.BD=BK.BC\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow BH.BD+CH.CE=BK.BC+KC.BC=\left(BK+KC\right)BC=BC^2\)












 Giúp mình làm bài này với ạ
Giúp mình làm bài này với ạ




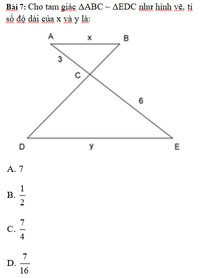



 giải giúp mình câu b, c với ạ!
giải giúp mình câu b, c với ạ!


