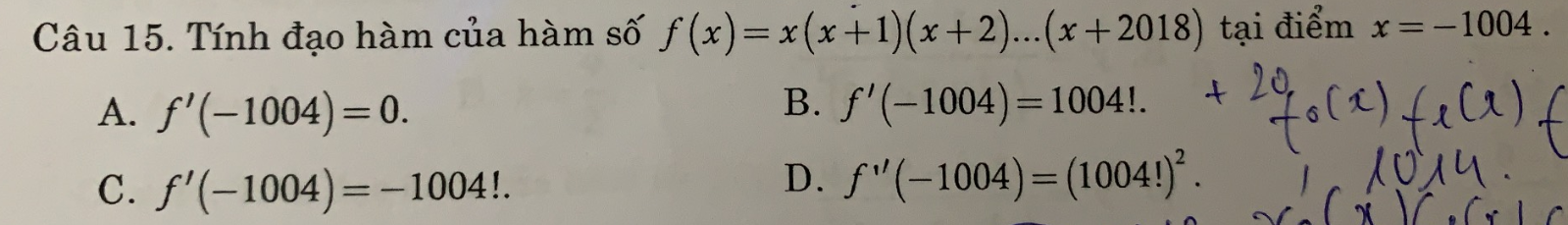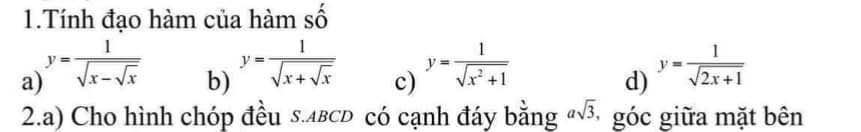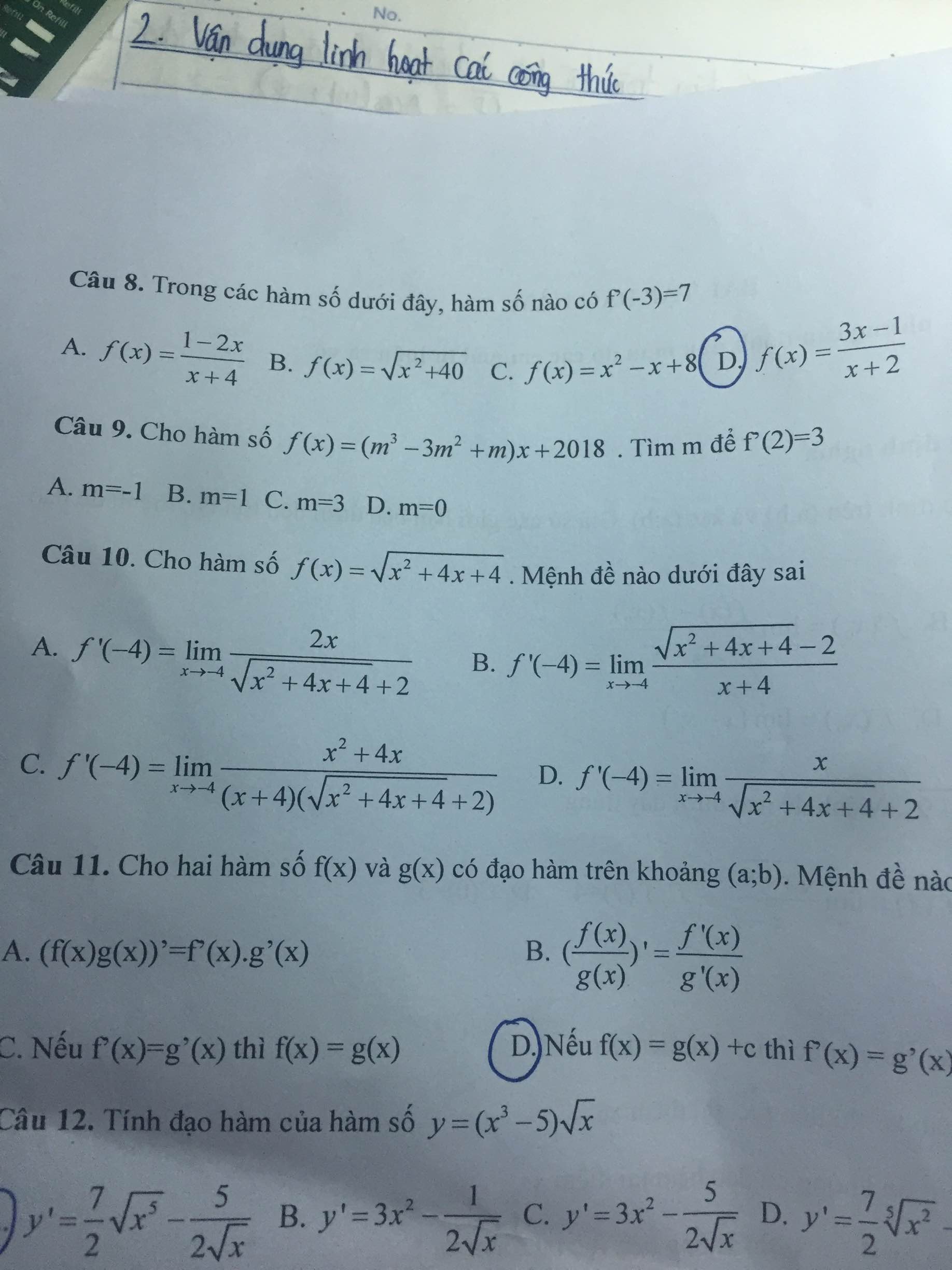Ta có : \(f\left(x\right)=x\left(x+1\right)\left(x+2\right)...\left(x+2018\right)\)
\(\Rightarrow f\left(-1004\right)=0\)
\(f'\left(-1004\right)=\)\(\lim\limits_{x\rightarrow-1004}\dfrac{f\left(x\right)-f\left(-1004\right)}{x+1004}\)
\(=\lim\limits_{x\rightarrow-1004}\dfrac{x\left(x+1\right)\left(x+2\right)...\left(x+2018\right)}{x+1004}\)
\(=\lim\limits_{x\rightarrow-1004}x\left(x+1\right)\left(x+2\right)...\left(x+1003\right)\left(x+1005\right)...\left(x+2018\right)\)
\(=-1004.\left(-1003\right).\left(-1002\right)...\left(-1\right)1.2...1014\)
\(=1014!.1004!\)
Đúng 2
Bình luận (0)
