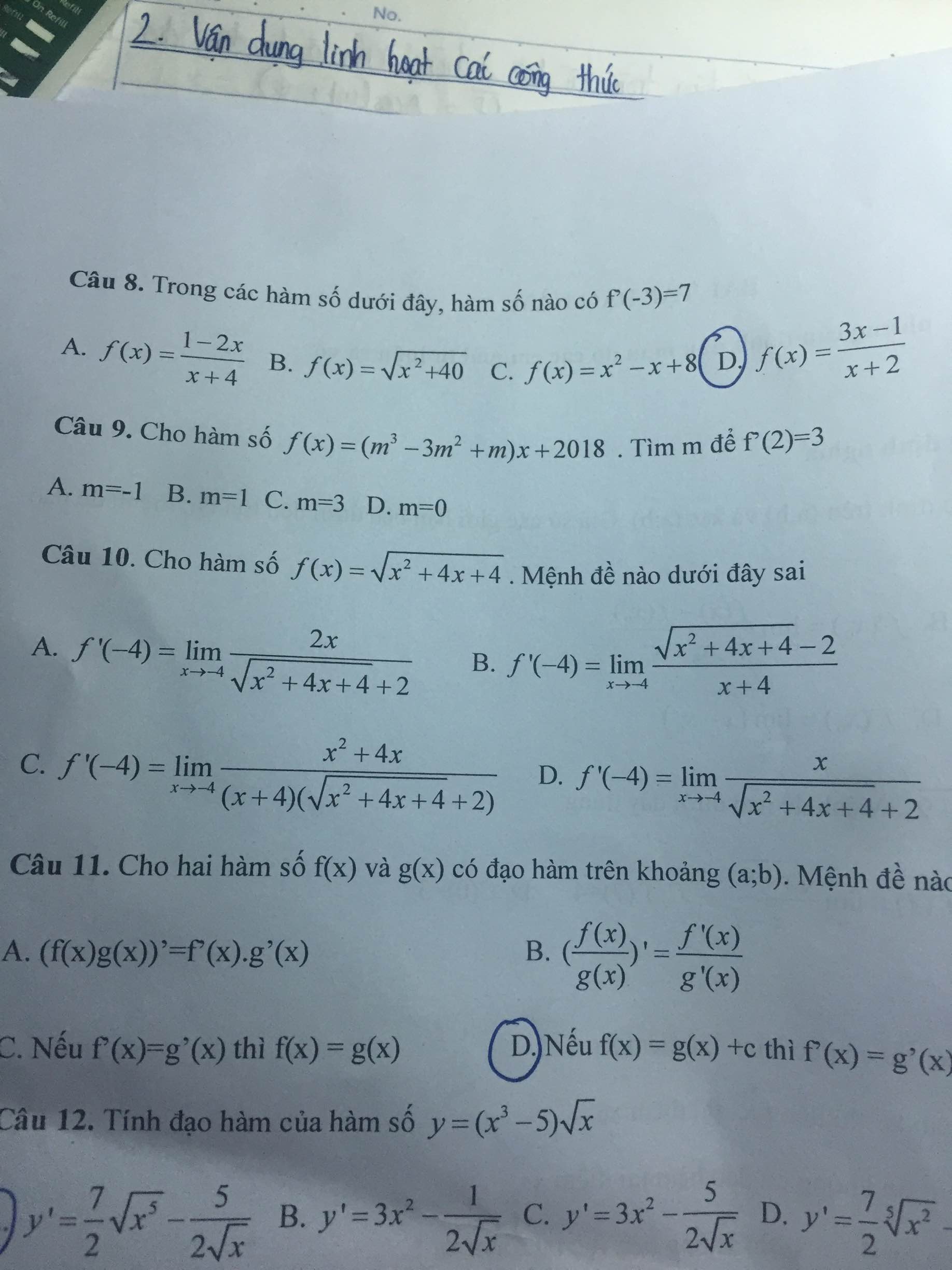9.
\(f'\left(x\right)=m^3-3m^2+m\) ; \(\forall x\)
\(f'\left(2\right)=m^3-3m^2+m=3\Leftrightarrow m\left(m^2+1\right)-3\left(m^2+1\right)=0\)
\(\Leftrightarrow\left(m-3\right)\left(m^2+1\right)=0\)
\(\Leftrightarrow m=3\)
10.
\(f'\left(x\right)=\dfrac{x+2}{\sqrt{x^2+4x+4}}=\dfrac{x+2}{\left|x+2\right|}=\left[{}\begin{matrix}1\left(x>-2\right)\\-1\left(x< -2\right)\end{matrix}\right.\)
Do \(-4< -2\Rightarrow f'\left(-4\right)=-1\)
Bây giờ chỉ cần kiểm tra 4 giới hạn kia cái nào có kết quả khác -1 là được
Trước hết lưu ý \(\sqrt{x^2+4x+4}=\left|x+2\right|=-x-2\) khi \(x\rightarrow-4\)
Do đó câu A là: \(\lim\limits_{x\rightarrow-4}\dfrac{2x}{-x-2+2}=-2\ne-1\)
Vậy đáp án A